Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 31

Considere o circuito da Figura 8.79. Determine vL(0+) e vc(0+).

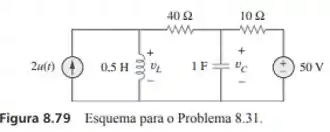
Passo 1

Vamos analisar cada instante separadamente.

No instante t = 0- o indutor se comportará como um curto-circuito e o capacitor como um circuito aberto. Assim, o circuito ficará da seguinte forma:

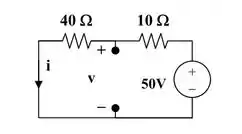
Aplicando a Lei de Ohm, teremos que:

i 0 - =   i 0 + = 50 10 + 40 = 1   A

E

v 0 - =   v 0 + = 50 - 10 ∙ 1 =   40   V  

∴ v C 0 + = 40 V

Passo 2

Para t = 0+ o circuito será igual ao da figura abaixo:

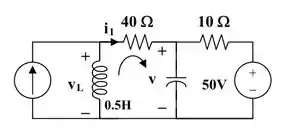
Calma, não pira com o tamanho do circuito.

Observa bem a malha que envolve o indutor e o capacitor. Tá pensando o mesmo que eu?

Siim, vamos aplicar as leis de Kirchoff!

Aplicando LKC:

  2 = i 0 + + i 1     →     2 = 1 + i 1

∴   i 1 = 1   A

Aplicando LKT:

  - v L + 40 i 1 + v 0 + = 0   →   v L =   40 + 40

∴ v L 0 + = 80   V

Resposta

v C 0 + = 40   V e v L 0 + = 80   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o circuito do Exemplo 8.7, determine, para t ≥ 0, (a) v(t) e (b) i C ( t ) .
Para o circuito do Exemplo 8.6, determine, para t ≥ 0, (a) v(t); (b) i R ( t ) e (c) i C ( t ) .
Admita que, no instante em que a fonte de corrente cc de 2 A é aplicada ao circuito da Figura P8.27, a corrente inicial no indutor de 25 mH seja 1 A e a tensão inicial no capacitor seja 50 V (positiva
As chaves 1 e 2 no circuito da Figura P8.38 são sincronizadas. Quando a chave 1 abre, a chave 2 fecha e vice-versa. A chave 1 esteve aberta por um longo tempo antes de fechar em t = 0 . Determine i L
A chave no circuito da Figura P8.46 esteve na posição a por um longo tempo. Em t = 0 , ela passa instantaneamente para a posição b . Determine i t para t ≥ 0 .