Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 62

Considere a figura e elabore um problema para ajudar outros estudantes a entenderem melhor o cálculo de tensões nodais no domínio s.

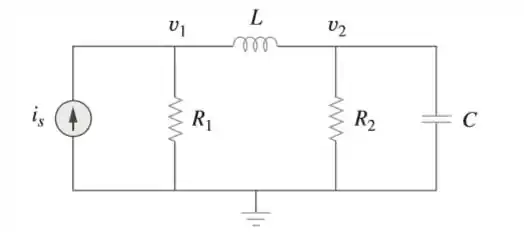
Passo 1

Vamos criar um problema com valores reais:

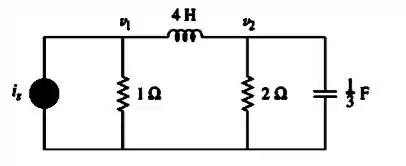
Passo 2

Agora, vamos passar esse circuito para o domínio de Laplace (domínio s):

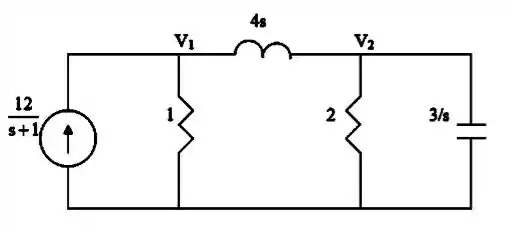
Passo 3

Agora podemos aplicar a lei de Kirchhoff no nó V 1 , vamos ter a equação 1:

12 s + 1 = V 1 1 + V 1 - V 2 4 s → 12 s + 1 = V 1 ( 1 + 1 4 s ) - V 2 4 s

E depois, vamos aplicar a lei de Kirchhoff no nó V 2 , vamos ter a equação 2:

V 1 - V 2 4 s = V 2 2 + s 3 V 2 → V 1 = V 2 ( 4 3 s 2 + 2 s + 1 )

Daí é só substituir a equação 2 na 1 e isolar o V 2 :

V 2 = 9 ( s + 1 ) ( s } 2 + 7 4 s + 9 8 )  

Passo 4

Separando em frações parciais teremos:

V 2 = 9 ( s + 1 ) ( s } 2 + 7 4 s + 9 8 )     = A s + 1 + B s + C s 2 + 7 4 s + 9 8

Agora basta encontrar A ,   B   e   C e encontrar V 2 .

A = 24

B =   - 24

C =   - 18

Daí, substituindo e completando o quadrado, teremos:

V 2 = 24 ( s + 1 ) - 24 s + 18 ( s 2 +   7 4 s + 9 8 ) = 24 ( s + 1 ) - 24 ( s + 7 8 ) ( s + 7 8 ) 2 + 23 64 + 3 ( s + 7 8 ) 2 + 23 64

Por Laplace utilizando a tabela de transformadas, teremos:

v 2 ( t )   = [ 24 e - t - 24 e - 0.875 t c o s ( 0.5995 t ) + 5.004 e - 0.875 t s e n ( 0.5995 t ) ] u ( t ) V

Passo 5

De forma semelhante, voltamos lá no Passo 3, e isolamos o V 1 e faremos o mesmo passo a passo:

V 1 = 9 ( 4 3 s 2 + 2 s + 1 ) ( s + 1 ) ( s 2 + 7 4 s + 9 8 )  

Passo 6

Separando em frações parciais teremos:

V 1 = 9 ( 4 3 s 2 + 2 s + 1 ) ( s + 1 ) ( s 2 + 7 4 s + 9 8 ) = D ( s + 1 ) + E s + F ( s 2 + 7 4 s + 9 8 )

Agora basta encontrar A ,   B   e   C e encontrar V 1 .

F = 6 - 3 4 D

D = 8

E = 4

F = 0

Daí, substituindo e compl, teremos:

V 1 = 8 ( s + 1 ) +   4 s ( s 2 + 7 4 s + 9 8 ) = 8 s + 1 + 4 ( s + 7 8 ) ( s + 7 8 ) 2 + 23 64 - 7 2 ( s + 7 8 ) 2 + 23 64

Por Laplace utilizando a tabela de transformadas, teremos:

v 1 ( t )   = [ 8 e - t + 4 e - 0.875 t c o s ( 0.5995 t ) - 5.838 e - 0.875 t s e n ( 0.5995 t ) ] u ( t ) V

Resposta

v 1 ( t )   = [ 8 e - t + 4 e - 0.875 t c o s ( 0.5995 t ) - 5.838 e - 0.875 t s e n ( 0.5995 t ) ] u ( t ) V

v 2 ( t )   = [ 24 e - t - 24 e - 0.875 t c o s ( 0.5995 t ) + 5.004 e - 0.875 t s e n ( 0.5995 t ) ] u ( t ) V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a frequência de ressonância de cada um dos circuitos da F i g u r a14.82
Considere o circuito ilustrado na Figura 14.85 e determine:A função de transferência H ω = V 0 ( ω ) / I ( ω ) A amplitude de H em ω 0 = 1r a d / s
Considere o circuito mostrado na Figura 14.84 e determine ω 0 , B e Q visto pela tensão no indutor.
Calcule o circuito da Figura 14.83 e determine:A frequência de ressonância ω 0 Z e n t ( ω 0 )
Considere a Figura 14.80 e elabora um probema para ajudar outros estudantes a entender melhor o fator de qualiade, a frequência de ressonância e a largura de banda de circuitos RLC.