Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.Problemas - Ex. 29
Determine e , de forma que o circuito seja um filtro passabaixas de primeira ordem , com ganho de 3. Altere em escala o resultado, para obter , usando um capacitor de .
Passo 1
E aí pessoal tudo belezinha? O enunciado pede que a gente determine e , de forma que o circuito seja um filtro passabaixas de primeira ordem , com ganho de 3.
Começamos esboçando o circuito elétrico do exercício, partiu?
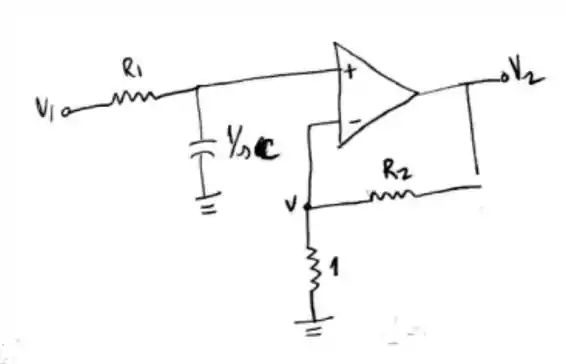
Passo 2
Agora temos que determinar o limite da relação das resistências , vem comigo 😊
Fazendo
Resposta
Exercícios de Livros Relacionados
Calcule a impedância do circuito da Fig. 10.15, se as funções no domínio do tempo representadas pelos fasores V e I são(a) v = - 30 cos 2 t + 16 sin 2 tV , i = 1,7 cos 2 t + 20 °A .(b) v = R e j
Se ω = 10 rad/s, calcule as funções no domínio do tempo representadas pelos fasores (a) - 5 + j 5 , (b) - 5 + j 12 , (c) 4 - j 3 , (d) - 10 , e (e) - j 5 .
Mostre que, calculando a função de rede H s = V 2 ( s ) / V 1 s , que o circuito é um filtro passa-faixa com ω 0 2 = 1 / ( L C ) , B = 1 / C e ganho = 1 . Escolha B e C de forma que B = 0.2 e ω 0 = 1
Mostre que, no caso geral, a função de rede na figura do Prob. 15.1 é dada por H s = V 2 s V 1 s = R L s s 2 + R L s + 1 L C Desta forma, por comparação com (15.22) e (15.25), mostre que o circuito é
Calcule H s = V 2 ( s ) / V 1 s e esboce as respostas em amplitude e fase. Mostre que o pico da amplitude e a fase zero ocorrem em ω = 4r a d / s .