Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.Problemas - Ex. 7
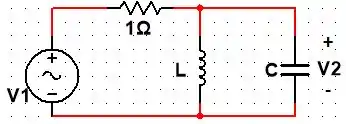
Mostre que, calculando a função de rede , que o circuito é um filtro passa-faixa com , e ganho . Escolha e de forma que e rad/s.
Passo 1
Eaeeee!! Vamos lá!
Primeiramente, vamos fazer a lei dos nós (simples de ver, pois só há um nó haha) de forma que:
Passo 2
Nesse sentido, percebemos que tem o formato de:
Logo, temos que:
Passo 3
Por fim, temos que o ganho é dado por:
Prooonto!! Viu? Simples! Só ir substituindo!! ;)
Resposta
Exercícios de Livros Relacionados
Calcule os seguintes números complexos: 5 - j 6 - 2 + j 8 - 3 + j 4 5 - j + ( 4 - j 6 ) 240 ∠ 75 ° + 160 ∠ - 30 ° 60 - j 80 ( 67 + j 84 ) ( 20 ∠ 32 ° ) 10 + j 20 3 + j 4 2 10 + j 5 16 - j 20
Calcule estes determinantes: 10 + j 6 2 - j 3 - 5 - 1 + j 20 ∠ - 30 ° - 4 ∠ - 10 ° 16 ∠ 0 ° 3 ∠ 45 ° 1 - j - j 0 j 1 - j 1 j 1 + j
Transforme as senoides a seguir em fasores: - 20 cos ( 4 t + 135 ° ) 8 s e n ( 20 t + 30 ° ) 20 cos 2 t + 15 s e n ( 2 t )
Obtenha as senoides correspondentes a cada um dos seguintes fasores: V 1 = 60 ∠ 15 °V ,ω = 1 V 2 = 6 + j 8V ,ω = 40 I 1 = 2,8 e - j π / 3A ,ω = 377 I 2 = - 0,5 - j 1,2A ,ω = 10 3
Calcule estes determinantes: 10 + j 6 2 - j 3 - 5 - 1 + j 20 ∠ - 30 ° - 4 ∠ - 10 ° 16 ∠ 0 ° 3 ∠ 45 ° 1 - j - j 0 j 1 - j 1 j 1 + j