Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 31

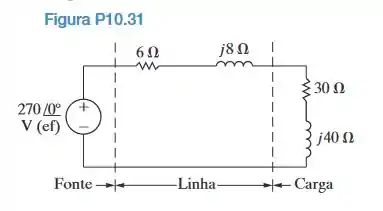
a) Determine a potência média dissipada na linha na Figura P10.31.

b) Determine a reatância capacitiva que, quando ligada em paralelo com a carga, fará com que esta se comporte como uma carga puramente resistiva.

c) Qual é a impedância equivalente da carga em (b)?

d) Determine a potência média dissipada na linha quando a reatância capacitiva está ligada à carga.

e) Expresse a perda de potência em (d) como uma percentagem da perda de potência determinada em (a).

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

A – Primeiramente, temos que notar que as impedâncias, então para o cálculo da corrente fornecida pela fonte de tensão, nós temos que

I = 270 6 + j 8 + 30 + j 40 = 270 36 + j 48

Desenvolvendo os termos

I = 2,7 - j 3,6

Passando para fasores, nós temos que

I = 4,5 ∠ - 53,13 °   A   r m s

Determinando a potência média P l 1 dissipada na impedância de linha

P l 1 = I 2 ( 6 )

Substituindo pela magnitude da corrente I

P l 1 = 4,5 2 6 = 121,5   W

Passo 2

B - Como o capacitor está conectado em paralelo à carga, é mais fácil determinar a admitância da carga primeiro, e com isso, temos que determinar a admitância da carga Y L

Y L = 1 Z L

Fazendo a substituição, nós temos que

Y L = 1 30 + j 40 = 0,012 - j 0,016   S

Logo, a reatância capacitiva é dada por

X C = 1 - 0,016 = - 62,5   Ω

Passo 3

C – A admitância equivalente Y e q é dada por

Y e q = Y L + Y c

Substituindo os valores, nós obtemos o seguinte resultado

Y e q = 0,012 - j 0,016 + 1 Z C = 0,012 - j 0,016 + 1 - 62,5 j

Logo

Y e q = 12   m S

Onde Z C é a impedância do capacitor, com isso, já podemos determinar a impedância do capacitor

Z e q = 1 Y e q

Logo, temos que

Z e q = 1 12 × 10 - 3 = 83,33   Ω

Passo 4

D – Determinando a corrente I   fornecida pela fonte de tensão

I = 270 6 + j 8 + 83,33 = 270 89,33 + j 8

Logo, desenvolvendo os termos, nós temos que

I = 3 - j 0,269

Transformando para as fasores,

I = 3,01 ∠ - 5,12 °   A ( r m s )

Determinando a potência média P l 2 dissipada pela impedância de linha

P l 2 = I 2 6

Fazendo a substituição

P l 2 = 3,01 2 6 = 54,36   W

Passo 5

E – Comparando as porcentagens, nós obtemos o seguinte resultado

%   p e r d a = P l 1 P l 2 ( 100   % )

Substituindo os valores, nós temos que

%   p e r d a = 54,36 121,5 100   % = 44,75   %

Assim, a adição do capacitor forneceu maior potência média à carga

%   p e r d a = 44,75   %

Resposta

a )   P l 1 = 121,5   W

b )   X c = - 62,5   Ω

c )   Z e q = 83,33   Ω

d )   P l 2 = 54,36   Ω

e )   %   p e r d a = 44,75   %  

Exercícios de Livros Relacionados

39- Um motor C A com impedância Z L = 4.2 + j 3.6Ω é alimentado por uma fonte de 220V ,60H z . ( a ) Determine F P ,P e Q . ( b ) Determine o capacitor necessário para ser conectado em paralelo com o
a) Se N 1 for igual a 1.000 espiras, quantas espiras deve ter o enrolamento N 2 do transformador ideal, no circuito apresentado na Figura P10.64, para que seja fornecida máxima potência média à carga
a) Determine a impedância de carga para o circuito da Figura P10.41 para a máxima transferência de potência média à carga, se ω = 8k r a d / s .b) Determine a máxima potência média fornecida à carga n
As três cargas do circuito da Figura P10.30 podem ser descritas da seguinte forma: a carga 1 é um resistor de 240Ω em série com uma reatância indutiva de 70Ω ; a carga 2 é uma reatância capacitiva de
a) Determine as seis correntes de ramo I a - I f no circuito da Figura P10.36.b) Determine a potência complexa em cada ramo do circuito.c) Confirme seus cálculos verificando se a potência média fornec