Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.1 - Ex. 1

Excite o circuito da Fig. 14.2 pela função complexa

v 1 = 25 e - t e j 2 t = 25 e - 1 + j 2 t

E demonstre que a pessoa forçada é

i 1 = ( 5 / - 53 , 1 ° ) e - 1 + j 2 t

Passo 1

Nessa questão ele pede para excitar o circuito

v 1 = 25 e - t e j 2 t = 25 e - 1 + j 2 t

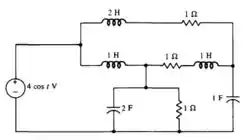
E demonstre que a pessoa forçada é

i 1 = ( 5 / - 53,1 ° ) e - 1 + j 2 t

Pode você ta com essa cara né? Hahaha fica tranquilo e vem

Passo 2

Sabendo que,

v 1 = 25 e - t e j 2 t = 25 e - 1 + j 2 t

Temos,

2 d i d t + 5 i = 25 e - t cos ⁡ 2 t

Sendo ela um ∆ < 0 (imaginária e complexa) temos,

y t = C 1 e α t cos ⁡ ( β t ) + C 2 e α t sin ⁡ ( β t )

i = e - t ( A cos ⁡ 2 t + B sin ⁡ 2 t )

Com isso sua excitação e todas suas possíveis derivadas, ficam

2 e - t - 2 A sin ⁡ 2 t - A cos ⁡ 2 t + 2 B cos ⁡ 2 t - B sin ⁡ 2 t + 5 e - t A cos ⁡ 2 t + B sin ⁡ 2 t

= 25 e - t cos ⁡ 2 t  

A = 3       e     B = 3

i = 5 e - t cos ⁡ ( 2 t - 53,1 ° ) A

Espero ter ajudado, bons estudos e até a próxima.

Resposta

i = 5 e - t cos ⁡ ( 2 t - 53,1 ° ) A

Exercícios de Livros Relacionados

Usando fasores, calcule a corrente em regime permanente i se v = 12 cos ⁡ ( 1000 t + 30 ° )V em (a) Fig. 10.9(a) para R = 4k Ω , (b) Fig. 10.11(a) para L = 15m H e (c) Fig. 10.13(a) para C = 1 2μ F .
Calcule v 1 da equação diferencial e use o resultado para calcular a resposta forçada para v para uma tensão de entrada de 34 cos ⁡ 4 tV .
Uma tensão complexa de entrada 10 e j 2 t + 25 ° V produz uma corrente de saída de 5 e j 2 t - 20 ° A. Calcule a corrente de saída se a tensão de entrada é (a) 40 e j 2 t + 60 ° V , (b) 20 c o s c o s
Calcule as representações fasoriais das funções no domínio do tempo (a) 10 cos ⁡ ( 5 t + 18 ° ) , (b) - 8 cos ⁡ 5 t + 6 sin ⁡ 5 t , (c) 18 sin ⁡ 5 t e (d) - 2 sin ⁡ ( 5 t - 10 ° )
Calcula v 1 da equação diferencial e use o resultado para calcular a resposta forçada para v para uma tensão de entrada de 34 cos ⁡ 4 tV .