Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.Problemas - Ex. 18
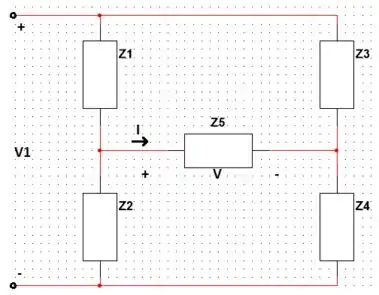
Mostre que se , , no circuito “ponte” mostrado, então e, portanto, todas as outras correntes e tensões permanecem inalteradas para qualquer valor de . Logo, ela pode ser trocada por um circuito aberto, um curto-circuito, etc. Neste caso, o circuito é dito como sendo uma ponte equilibrada.
Passo 1
Já sei! Na primeira lida que vc deu na questão deve ter ficado:
E se eu te falar que isso é muito simples de entender?? Quer apostar??? Então vem comigo aqui haha.
Olha, para ficar mais fácil a análise, vamos nomear os nós da figura da seguinte forma:
Passo 2
Primeiramente, observando a figura, temos que . Até aí beleza né?
Ainda, o enunciado da questão diz que , ou seeeja, a queda de tensão será igual nos dois pois estão em paralelo através do nó .
Tá... mas o que isso implica? Se liga:
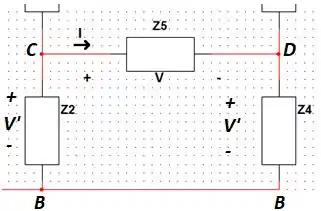
Como a diferença de potencial em será igual em (fazendo como referência), então, não há diferença de potencial entre . Logo, não passa corrente em .
Viu como é simples? Só vem pra mais outra hehe