Mostre que na figura do Prob. 15.1
Faça e e mostre que o resultado é um filtro passa-altas com corte . O ganho de um filtro passa-altas é definido como o limite de sua função de transferência quando . Note que, neste caso, o ganho é 1 .Mostre, calculando a função de transferência , a resposta em amplitude, o ganho (ver o Prob. 15.21) e o ponto de corte , que o circuito é um filtro passa-altas de segunda ordem.

Passo 1
O enunciado pede que a gente mostre, calculando a função de transferência , a resposta em amplitude, o ganho (ver o Prob. 15.21) e o ponto de corte , que o circuito é um filtro passa-altas de segunda ordem.
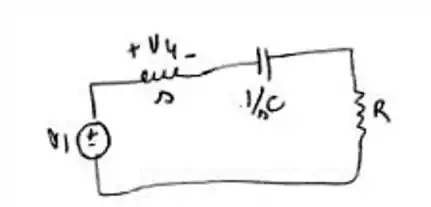
Passo 2
F. corte