Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 32
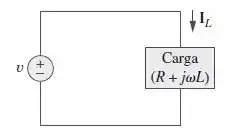
Usando a Figura , elabore um problema para ajudar outros estudantes a entender melhor a relação de fasores para os elementos de circuitos.
Passo 1
Galera, vamos resolver a seguinte questão:
“Se a carga for igual a e a tensão de entrada igual a , encontre a corrente .”
Bom, a corrente pode ser calculada através da seguinte expressão:
Vamos passar a impedância para a forma polar!
Assim, . Substituindo na equação da corrente, temos:
Convertendo o resultado para o domínio do tempo:
Resposta
A corrente é igual a:
Exercícios de Livros Relacionados
Uma tensão v t = 100 cos ( 60 t + 20 ° )V é aplicada a uma associação em paralelo entre um resistor de 40k Ω e um capacitor de 50μ F . Encontre as correntes em regime estacionário no resistor e no c
Qual é o valor de ω que fará que a resposta forçada, v 0 , na figura 9.41 , seja zero?
Projete um circuito que transforme uma entrada de tensão senoidal em uma saída de tensão cossenoidal.
Projete um circuito R L para fornecer um deslocamento de fase com avanço de 90 ° .
Para os pares de sinais a seguir, determine se v 1 está avançada ou atrasada em relação a v 2 e de quanto. av 1 = 10 ⋅ cos 5 t - 20 ° , v 2 = 8 ⋅ cos 5 t bv 1 = 19 ⋅ cos 2 t + 90 ° , v 2 = 6 ⋅ s