Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.Problemas - Ex. 38

Mostre que a função de rede V 3 / V 1 na figura do Prob. 15 . 36 é dada por

V 3 V 1 = 1 / L C s 2 + ( R / L ) s + ( 1 / L C )

Faça R = 1 Ω , L = 1 / 2 H e C = 2   F , e mostre que o resultado é um filtro passa-baixas e ω c = 1 r a d / s , calculando a resposta em amplitude.

Passo 1

Fala aí pessoal o exercício quer que a gente mostre que a função de rede V 3 / V 1 na figura do Prob. 15.36 é dada por

V 3 V 1 = 1 / L C s 2 + ( R / L ) s + ( 1 / L C )

Esboçando o circuito temos 😊

I = V 1 s L + 1 s C + R = V 1 s 2 L C + 1 + s R C s C

V s = 1 s C ⋅ I = 1 D C ⋅ V + D C s 2 L C + s R C + 1 ⇒ V 3 V 1 = 1 / L C s 2 + s R / L + 1 / L C

R = 1             L = 1 2                                 C = 2

W ω j = 1 - ω 2 + ω j 2 + 1 ⇒ 1 1 - ω 2 + j ( 2 ω )

H ω j = 1 1 - ω 3 2 + ( 2 ω ) 2

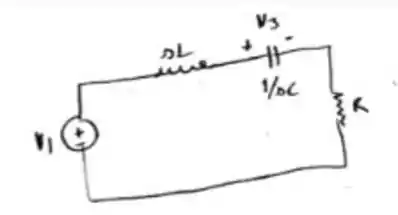
Passo 2

ω → 0 H ω j = 1 ω → ∞ N ω j = 0

F de corte

| H ( ω j ) | = 1 / 2 ∣ H ( j w ) ∣ m a x : 1 1 - ω 0 2 2 + 2 ω 2 = 1 2 ⋅ 1

⇒ 1 - 2 ω 0 2 + ω 0 4 + 2 ω 0 2 = 2 ⇒ ω 0 4 = 1 ⇒ ω e = 1 r a d / s

Resposta

ω e = 1 r a d / s

Exercícios de Livros Relacionados

Usando fasores, calcule a corrente em regime permanente i se v = 12 cos ⁡ ( 1000 t + 30 ° )V em (a) Fig. 10.9(a) para R = 4k Ω , (b) Fig. 10.11(a) para L = 15m H e (c) Fig. 10.13(a) para C = 1 2μ F .
Usando fasores, calcule a corrente em regime permanente i se v = 12 cos ⁡ ( 1000 t + 30 ° )V em (a) Fig. 10.9(a) para R = 4k Ω , (b) Fig. 10.11(a) para L = 15m H e (c) Fig. 10.13(a) para C = 1 2μ F .
Calcule v 1 da equação diferencial e use o resultado para calcular a resposta forçada para v para uma tensão de entrada de 34 cos ⁡ 4 tV .
Uma tensão complexa de entrada 10 e j 2 t + 25 ° V produz uma corrente de saída de 5 e j 2 t - 20 ° A. Calcule a corrente de saída se a tensão de entrada é (a) 40 e j 2 t + 60 ° V , (b) 20 c o s c o s
Calcule as representações fasoriais das funções no domínio do tempo (a) 10 cos ⁡ ( 5 t + 18 ° ) , (b) - 8 cos ⁡ 5 t + 6 sin ⁡ 5 t , (c) 18 sin ⁡ 5 t e (d) - 2 sin ⁡ ( 5 t - 10 ° )