Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 83
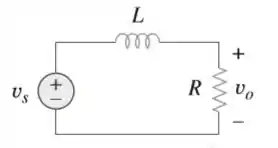
Observe o circuito na figura. Determine:
- A resposta do circuito ao impulso .
- A resposta do circuito a um degrau unitário.
Passo 1
Na letra a, vamos começar achando (domínio da frequência):
Note que esse é a função de transferência do circuito multiplicado pelo Laplace do impulso (que é 1), por isso não aparece ali.
Agora, basta passar isso para o domínio do tempo:
Sabemos que:
então
Passo 2
Agora, na letra b, vamos fazer a função de transferência com um degrau de entrada, cuja transformada de Laplace é .
Teremos:
Passo 3
Separando em frações parciais:
e
Substituindo:
Agora basta aplicar a transformada inversa, sabendo que :
Resposta
a)
b)
Exercícios de Livros Relacionados
Os parâmetros do circuito da Figura P12.29 são R = 4 kV, L = 400 mH e C = 156,25nF. Se Vcc = 120 V, determine vo(t), para t $ 0.
a) Escreva as duas equações diferenciais simultâneas que descrevem o comportamento do circuito mostrado na Figura P12.32, em termos das correntes de malha i 1 e i 2. b) Determine as transformadas de L
Use os teoremas do valor inicial e do valor final para verificar os valores inicial e final da corrente e da tensão no Problema 12.30.
A chave no circuito da Figura P12.29 esteve na posição a pôr um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. Deduza a equação íntegro-diferencial que governa o comportamento da
Determine a transformada de Laplace para (a) e (b). a) f t = d d t e - a t c o s w t b) f t = ∫ 0 - 1 e - a xs i nw xd x c) Verifique os resultados obtidos em (a) e (b), primeiro executando a operação