Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 68
Obtenha no circuito com AOP da figura:
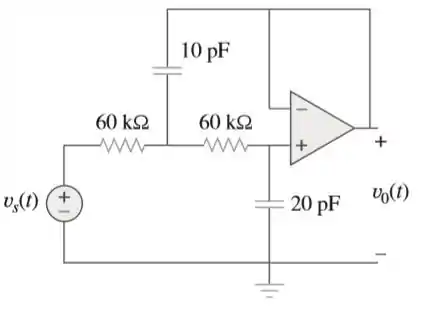
Passo 1
Vamos desenhar o circuito no domínio da frequência (domínio s):
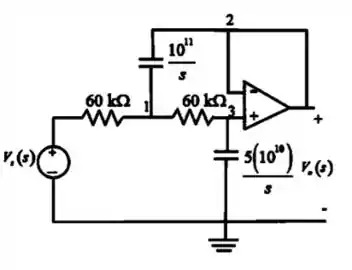
Passo 2
Aplicando a lei das correntes de Kirchhoff no nó 1, temos:
Aplicando a lei das correntes de Kirchhoff no nó 2:
Aplicando a lei das correntes de Kirchhoff no nó 3:
Passo 3
A partir destas equações, substituímos a equação da malha 2 e da malha 3 na da malha 1, e assim, podemos isolar apenas e:
Resposta
Exercícios de Livros Relacionados
a) Dado que F(s) = l {f (t)}, mostre que - d F(s)/ds = l {t f (t)}. b) Mostre que (-1)^nd^nF(s) ds^n = l{t^nf(t)} . c) Use o resultado de (b) para determinar e l{t^5}, l{tsenbt} e l{te^-tcosh t}.
Os parâmetros do circuito da Figura P12.30 são R = 2 kV; L = 1,6 H e C = 5 mF. Se Vcc for 56 V, determine a) vo(t), para t $ 0. b) i o(t), para t $ 0.
Determine f(t) para cada uma das seguintes funções:
Use os teoremas do valor inicial e do valor final para verificar os valores inicial e final da corrente e da tensão no Problema 12.27.
Os parâmetros do circuito da Figura P12.31 são R = 4.000 V; L = 40 mH e C = 15,625 nF. Se I g(t) for 150 mA, determine v2(t).