Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 36

Obtenha v(t) e i(t) para t > 0 no circuito da Figura 8.84.

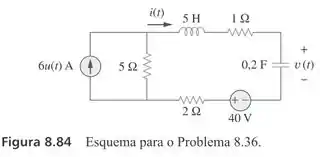
Passo 1

A primeira coisa que devemos fazer é analisar o circuito para os instantes t = 0- e t > 0.

Em t = 0-:

  6 u t = 0

Então:

i 0   =     0 e     v ( 0 )     =     4 0   V

Passo 2

Quando t > 0, teremos um circuito RLC série como mostra a figura abaixo:

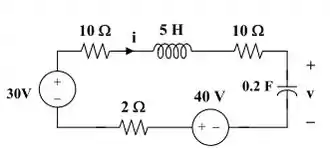
Então, precisamos calcular os valores de α, ωo e S:

α = R 2 L = 2   +   5   +   1 2 ∙ 5 = 0,8

ω o =   1 L C = 1 5 ∙ 0,2 = 1

Descobrimos que α

s 1,2 = - α ± α 2 - ω o 2 = - 8 ± j 0.6

Passo 3

Já podemos partir para a nossa equação de resposta natural. Ela é da seguinte forma:

v ( t ) =   V s   + [ A c o s 0.6 t + B s i n 0.6 t e - 0.8 t ]

V s = 30 + 40 = 70   V

Passo 4

Estamos quase lá, mas ainda não sabemos os valores de A e B. Nossa missão agora é calculá-los.

Vamos analisar as equações que já encontramos, mas dessa vez, no instante t = 0:

v 0 = 40 = 70 + A         →           A = - 30

i ( 0 )     =   C d v 0 d t     =     0  

Mas:

d v d t = [ – 0.8 A c o s 0.6 t + B s i n 0.6 t e – 0.8 t ] + [ 0.6 – A s i n 0.6 t + B c o s 0.6 t e – 0.8 t ]

d v 0 d t =   – 0.8 A + 0.6 B    

Substituindo A:

  B = 0.8 ∙ – 30 0.6                 →               B =   – 40  

Portanto:

v ( t ) = { 70   – [ 30 c o s 0.6 t + 40 s i n 0.6 t e – 0.8 t ] }     V

Passo 5

Por fim, vamos encontrar i(t).

Já estamos carecas de saber que:

i   = C d v d t

Como nós já calculamos a derivada de v(t), só nos resta multiplicar aquilo tudo pelo valor da capacitância, ficando assim:

  i = 0.2 { [ 0.8 30 c o s 0.6 t + 40 s i n 0.6 t e - 0.8 t ] + [ 0.6 30 s i n 0.6 t – 40 c o s 0.6 t e - 0.8 t ] }

i t = 10 s i n 0.6 t e - 0.8 t   A

Resposta

v ( t ) = { 70   – [ 30 c o s 0.6 t + 40 s i n 0.6 t e – 0.8 t ] }     V

E

i t = 10 s i n 0.6 t e - 0.8 t   A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura 8.124 mostra um circuito típico de oscilador com diodo túnel. O modelo para o diodo é um resistor não linear com i D = f ( v D ) , ou seja, a corrente no diodo é uma função não linear da tens
Para o circuito da Figura 8.62, determine:(a) i ( 0 + ) e v ( 0 + ) (b) d i ( 0 + ) / d t e d v ( 0 + ) / d t (c) i ( ∞ ) e v ( ∞ )
Para os valores de i 2 0 + , d i 2 0 + d t e v g dados no Ex. 9.1.2, mostre que i 2 no Ex. 9.1.1 é dado por i 2 = - 4 e - t + 7 e - 2 t - e - 6 t A (Sugestão: Substitua a resposta na equação diferenci
Assuma v g = 14 e - 2 tV , i 1 0 + = 6 A e i 2 0 + = 2 A no Ex. 9.1.1, e calcule d i 2 ( 0 + ) / d t (o valor de d i 2 / d t em t = 0 + ).
Calcule a equação que satisfaz a corrente de malha i 2