Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas Abrangentes - Ex. 83

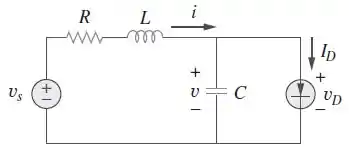
A figura 8.124 mostra um circuito típico de oscilador com diodo túnel. O modelo para o diodo é um resistor não linear com i D = f ( v D ) , ou seja, a corrente no diodo é uma função não linear da tensão no diodo. Deduza a equação diferencial para o circuito em termos de v e i D .

Passo 1

Pessoal, para o circuito dado, a tensão no resistor R é dada por:

v R = i R … 1

A tensão no indutor é dada por,

v L = L d i d t … ( 2 )

E a corrente que passa pelo capacitor é dada por:

i C = C d v d t … ( 3 )

Passo 2

Aplicando a lei dos nós no nó entre o capacitor e o indutor,

- i + i C + I D = 0

i = i C + I D

Da equação ( 3 ) ,

i = C d v d t + I D … 4

Aplicando a lei das malhas na malha da esquerda,

- v S + v R + v L + v = 0

Substituindo os valores encontrados em ( 1 ) e ( 2 ) :

v s = i R + L d i d t + v … ( 5 )

Passo 3

Substituindo a equação ( 4 ) em ( 5 ) ,

v S = R C d v d t + I D R + L d d t C d v d t + I D + v

v S = R C d v d t + I D R + L C d 2 v d t 2 + L d I D d t + v

Dividindo por L C e rearranjando a equação, temos:

d 2 v d t 2 + R L d v d t + R L C I D + 1 C d I D d t + v - v S L C = 0

Resposta

A equação diferencial é igual a:

d 2 v d t 2 + R L d v d t + R L C I D + 1 C d I D d t + v - v S L C = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o circuito da Figura 8.97 , determine i ( t ) para t0 .
Determine a tensão de saída v 0 ( t ) no circuito da Figura 8.94 .
Usando a Figura 8.9 3 , elabore um problema para ajudar outros estudantes a entenderem melhor a resposta a um degrau de um circuito R L C em paralelo.
Determine i ( t ) para t0 no circuito da Figura 8.96 .
Dado o circuito da Figura 8.95 , determine i ( t ) e v ( t ) para t0 .