Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas Abrangentes - Ex. 76

76. Repita o problema 2.75   para o divisor de oito vias mostrado na figura 2.136 .

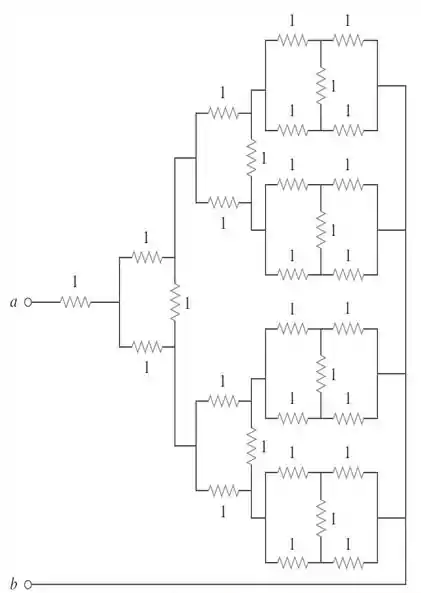
Passo 1

Bom! Do problema 2.75 obtemos que a resistência equivalente para a seguinte parte destacada em vermellha...

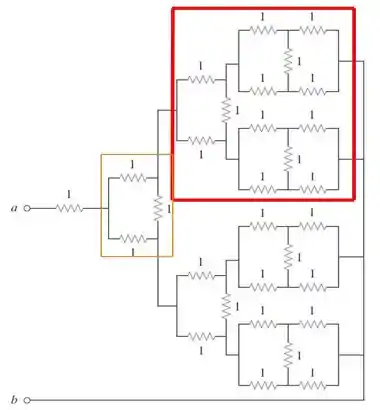
Vale 1   Ω ...

Essa parte alaranjada do nosso circuito tá bem fácil de entender! É uma configuração triangular, ou em delta, que não tá muito legal da gente trabalhar. Por isso, vamos fazer a transformação de delta para estrela:

Como todos tem a mesma resistência, vamos fazer o cálculo apenas uma única vez. Pra isso, basta usar as fórmulas já prontas para a conversão de um circuito ∆ em Y . São elas:

R a n = R 2 R 3 R 1 + R 2 +   R 3

R b n = R 1 R 3 R 1 + R 2 +   R 3

R c n = R 1 R 2 R 1 + R 2 +   R 3

Onde:

R 1 = 1   Ω

R 2 = 1   Ω

R 3 = 1   Ω

O que nos leva ao seguinte resultado:

R a n = 1 ⋅ 1 1 + 2 + 1 Ω

R b n = 1 ⋅ 1 1 + 2 + 1 Ω

R c n = 1 ⋅ 1 1 + 2 + 1 Ω

R a n = 1 3   Ω

R b n = 1 3   Ω

R c n = 1 3   Ω

Passo 2

E com isso, chegamos ao seguinte circuito:

Nós queremos descobrir o valor da resistência equivalente R e q ao longo de a - b . Ora bolas! Tá na cara que ela é dada por:

R e q = 1   Ω + 1 3 Ω + 1 3 Ω + 1 Ω | | 1 3 Ω + 1 Ω

R e q = 1   Ω + 1 3 Ω + 1 3 Ω + 1 Ω | | 1 3 Ω + 1 Ω

R e q = 1   Ω + 1 3 Ω + 4 3 Ω ⋅ 4 3 Ω 4 3 Ω + 4 3 Ω

R e q = 1   Ω + 1 3 Ω + 2 3 Ω

R e q = 1   Ω + 1 3 Ω + 2 3 Ω

R e q = 1   Ω + 1   Ω

R e q = 2   Ω

Resposta

R e q = 2   Ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule i 1 e i 2 .
Calcule v e a potência entregue pela fonte.
a) Mostre que a solução do circuito na Figura 3.9 (veja Exemplo 3.1) satisfaz a lei de correntes de Kirchhoff nas junções x e y.b) Mostre que a solução do circuito na Figura 3.9 satisfaz a lei das ten
Para cada um dos circuitos mostrados na Figura P3.4, a) determine a resistência equivalente vista pela fonte, b) determine a potência fornecida pela fonte
Determine a corrente e a potência fornecidas pela fonte de 40V no circuito do Exemplo 3.7 (Figura 3.32) substituindo o Δ inferior ( 25 ; 37,5e40Ω ) por seu Y equivalente.