Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.5 - Ex. 2

Resolva o Ex. 8.5.1, se v g = 50 e - 3 t   V

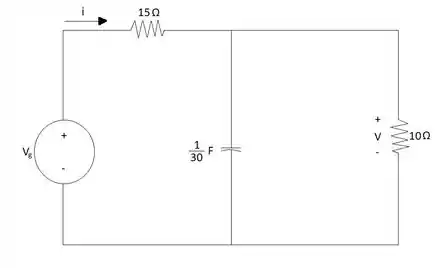
Passo 1

Opa! Vejo que temos mais uma questão a ser resolvida. Ajudarei vocês nessa, vamos lá!

Esta questão apresenta o mesmo circuito da questão anterior ao livro do Johnson, a única coisa que mudou foi o valor da fonte de tensão, sendo assim aplicamos a análise nodal para encontrar a expressão matemática que devemos resolver:

v 1 = v g = 50 e - 3 t   V

v - v 1 15 + C d v d t + v 10 = 0

Resolvendo esse sistema de equações chegaremos na seguinte expressão matemática:

d v d t + 5 v = 100 e - 3 t

Passo 2

Agora encontraremos o valor de v ( 0 ) sendo que nos foi dado o valor de i ( 0 ) , mas desta vez a fonte de tensão varia com o tempo, só que como queremos em t = 0 podemos escrever da seguinte forma:

v 0 - v 1 15 = - 1

v 0 - 50 e - 3.0 15 = - 1

v 0 = 35   V

Dando continuidade à resolução da questão, se resolve a equação diferencial de 1 ordem encontrada com a análise nodal. Como se trata de uma resolução matemática e nesta parte estamos focando apenas na parte elétrica pularemos essa etapa e obteremos a seguinte expressão:

v t = 50 e - 3 t + C e - 5 t

Passo 3

Para encontrar a expressão final de v t precisamos encontrar o valor da constante C usando o valor de v 0 :

35 = 50 + C

C = - 15

Substituindo o valor na expressão temos:

v t = 50 e - 3 t - 15 e - 5 t   V

Resposta

v t = 50 e - 3 t - 15 e - 5 t   V