Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 6.Problemas - Ex. 8
Sabe-se que a corrente no indutor de 50 mH da Figura P6.8 é 100 mA para t , 0. A tensão
do indutor para t $ 0 é dada pela expressão
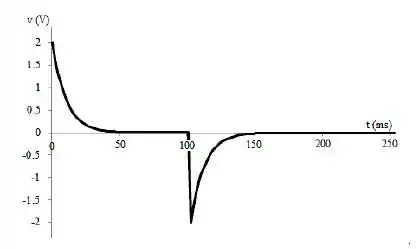
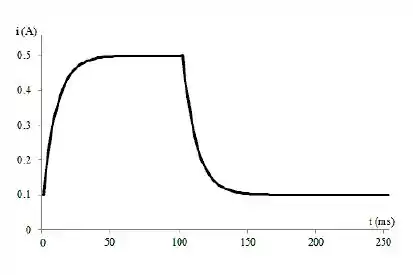
Faça um gráfico de vL(t) e iL(t) para .
Passo 1
Falaaa, pessoal! Como vocês estão?
Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre circuitos elétricos!
Para o primeiro intervalo, temos que:
Uma vez que essa relação é simplificada, chegamos a equação que representa o intervalo:
Passo 2
Para o segundo intervalo por sua vez, temos:
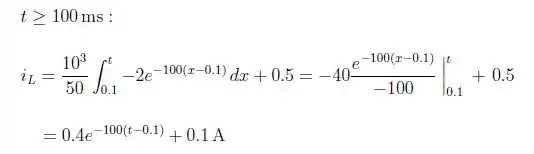
Dessa forma, é só utilizarmos os dados pra gerar os gráficos pedidos na questão.
Resposta
Exercícios de Livros Relacionados
Um indutor de 2-mH tem uma tensão v = 2 cos 1000 t V com i(0) = 1,5 A. Calcule a energia armazenada no indutor em t = π/6 ms
Na Fig. 7.10, seja I = 5 A, R1 = 6𝝮, R2 = 4 𝝮, L = 2H, e i1(0-) = 2 A. Se a chave é aberta em t = O-, encontre iL(0-), iL(0+), i1(0+) e diL(0+)/dt.
Calcule os valores máximo e mínimo da indutância que pode ser obtida usando-se 10 indutores de 10-mH.
Deduza uma equação para a divisão de corrente entre dois indutores em paralelo, sem corrente inicial, por meio de i1 e i2.
Calcule a indutância equivalente. (Os valores dos indutores são dados em mH.)