Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.Problemas - Ex. 18

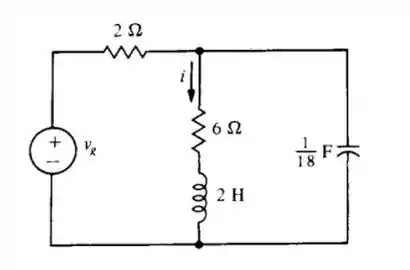
Substitua tudo no circuito fatorial correspondente, exceto o indutor, por seu circuito equivalente Thévenin e use o resultado para calcular a resposta forçada i , se v g = 4 e - 3 t c o s ⁡ 3 t   V

Passo 1

Vamos calcular a a resposta forçada i , se v g = 4 e - 3 t c o s ⁡ 3 t   V .

Começamos esboçando o circuito :)

V g = 4 e - 3 t c o s ⁡ 3 T V

V g s = 4 ∠ 0                 s = - 3 + 3 j

V = V g ⋅ 18 s ⋅ ( 6 + 2 s ) 2 + 18 s ( 6 + 20 ) ⇒ 18 ( 6 + 2 s ) / s ( 2 s + 18 ( 6 + 2 s ) ) / s V 8 ⇒ 36 s + 108 38 s + 108 V g

i = V 6 + 2 s = 36 s + 108 ( 6 + 2 s ) ( 38 s + 108 ) V g

i = 36 ( - 3 + 3 j ) + 108 ( 6 + 2 ( - 3 + 3 j ) ) ( 38 ( - 3 + 3 j ) + 108 ) 4 = 22 < 178 , 6 ∘

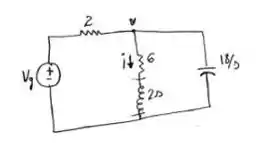
Resposta

I= 22 < 178 , 6 ∘

Exercícios de Livros Relacionados

Faça a função de rede da Fig. 15.1 ser H = I L / I 1 , onde I L e a corrente fasorial no indutor, em sentido para baixo. Mostre que H s = 1 L C s 2 + 1 R C s + 1 L C e que H M A X = 1 , ocorrendo em ω
Use o conceito de fasor para combinar as seguintes funções senoidais em uma única expressão trigonométrica: a) y = 30 cos(200t - 160°) + 15 cos(200t + 70°), b) y = 90 sen(50t - 20°) + 60 cos(200t - 70
Empregue o método do Ex. 14.1.3 para calcular a resposta forçada v , se d 3 v d t + 6 d 2 v d t 2 + 11 d v d t + 6 v = i Onde i = 4 e - 2 t cos ⁡ ( t - 60 ° )
Mostre que, sei 1 e a resposta a v 1 na equação 2 d i d t + 5 i 1 = v 1 então Re i 1 e a resposta a Re v 1 Aplique este resultado as funções do Ex. 14.1.1 para obter i dado por (14.6).
Excite o circuito da Fig. 14.2 pela função complexa v 1 = 25 e - t e j 2 t = 25 e - 1 + j 2 t E demonstre que a pessoa forçada é i 1 = ( 5 / - 53 , 1 ° ) e - 1 + j 2 t