Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 9.Problemas - Ex. 9
A tensão aplicada ao circuito mostrado na Figura 9.5 em t = 0 é 75 cos (4.000t - 60°) V. A resistência do circuito é 400 V e a corrente inicial no indutor de 75 mH é igual a zero. a) Determine i(t) para t $ 0. b) Escreva as expressões para as componentes transitórias e de regime permanente de i(t). c) Determine o valor numérico de i depois de a chave estar fechada por 750 ms. d) Quais são a amplitude máxima, a frequência (em radianos por segundo) e o ângulo de fase da corrente de regime permanente? e) De quantos graus é a defasagem entre a tensão e a corrente de regime permanente?
Passo 1
Saaaalve galerinha. Tudo bem com vocês? Então bora lá. Pro item a), temos que os valores numéricos dos termos da eq da 9.8 são:
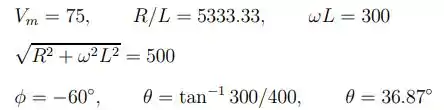
Substituindo esses valores na equação da 9.9:
Passo 2
Aqui no item b), o componente transiente:
Componente do estado estacionário:
Já no item c), temos que por direta substituição na equação 9.9 no item a,
Passo 3
No item d) resolvendo por partes, tudo está na equação! Temos:
No item e), pra finalizar, temos que a tensão corrente atrasa a tensão em 36.87 graus.