Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 88
Use o PSpice ou MultiSim para determinar e no circuito da Figura a seguir:
Passo 1
Bom, galera, como os componentes já estão no domínio do tempo. Assim, vamos usar o PSpice para determinar e :
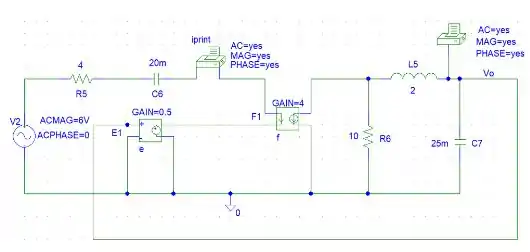
Depois de simular o circuito, o arquivo de saída deverá conter a frequência da fonte e os atributos que escolhemos imprimir, como o módulo da tensão e o ângulo e a corrente. Assim, conseguimos os valores:
Assim, podemos escrever a resposta como:
Convertendo para o domínio do tempo:
Resposta
A tensão e a corrente são iguais a:
Exercícios de Livros Relacionados
O capacitor de 0,5 mF no circuito visto na Figura P9.69 é substituído por um capacitor variável. O capacitor é ajustado até que a tensão de saída esteja 135° adiantada em relação à tensão de entrada.
No circuito da Figura P9.63, suponha que va = 10 cos 16.000t V, vb = 20 cos 4.000t V. a) Qual é a técnica de análise de circuitos que deve ser utilizada para determinar a expressão de regime permanent
3 Use o método das correntes de malha para determinar a expressão de regime permanente para vo(t) no circuito da Figura P9.63, se va = 18 sen 4.000t V, vb = 12 cos 4.000t V
O circuito da Figura P9.41 está em regime permanente senoidal. O capacitor é ajustado até que a corrente i g fique em fase com a tensão senoidal vg. a) Especifique a capacitância em microfarads, se vg
Use o método das tensões de nó para determinar a tensão fasorial V g no circuito da Figura P9.55.