Um ioiô de massa em seu movimento vertical, atinge uma altura mínima em relação ao solo igual a quando o fio está totalmente esticado. Quando o ioiô volta a mão da criança, ele tem uma altura igual a . Qual é a variação da energia potencial gravitacional nesse movimento?
Passo 1
Vamos começar fazendo um desenho esquemático do menino jogando o ioiô
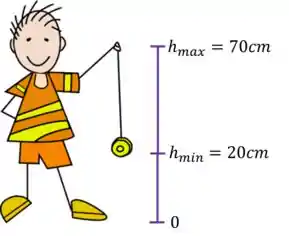
Você lembra que a energia potencial gravitacional era descrita pela equação:
Ou seja, dependia da massa , da aceleração da gravidade que é a mesma para todos os seres do planeta e da altura que esse corpo está.
Passo 2
Vamos pensar quando o ioiô está com seu fio completamente esticado, ele está a uma altura:
Percebe que a altura está em centímetros e não em metros, mas a nossa fórmula necessita que a altura esteja em metros, então faremos essa transformação.
Para transformar de centímetros em metros é só dividir por
A massa do ioiô é igual a:
Mais uma vez a unidade está errada, precisamos que ela esteja em quilogramas, então precisamos dividir por :
Considerando que estamos usando o ioiô na Terra e que a aceleração da gravidade de toda a superfície terrestre seja igual a:
Podemos substituir todos esses valores na fórmula da energia potencial gravitacional:
Encontraremos então a energia potencial mínima:
Fazendo o produto entre essas três parcelas, encontramos:
Passo 3
Quando o fio do ioiô está completamente enrolado, ele atinge uma altura máxima igual a:
Novamente a altura está em centímetros, dividindo por chegaremos ao valor em metros:
Mantemos o mesmo ioiô, logo a massa é igual a:
Enquanto a gravidade também continua a mesma:
Podemos substituir todos esses valores na fórmula da energia potencial gravitacional:
Encontraremos então a energia potencial mínima:
Fazendo o produto entre essas três parcelas, encontramos:
Passo 4
O enunciado nos pede qual é a variação da energia potencial gravitacional durante o movimento, o que nada mais é do que a diferença entre a energia máxima e a energia mínima:
Substituindo os valores que encontramos para a energia máxima e mínima:
Essa é a resposta final que tanto desejamos!