Uma mola é deslocada da sua posição de equilíbrio; sendo a constante elástica desta mola equivalente à , determine a energia potencial elástica associada a esta mola em razão desta deformação.
Passo 1
Faaala galera, tudo tranquilo? Preparados para mais uma questão de energia potencial? Então bora lá!
Vamos começar desenhando o que está acontecendo
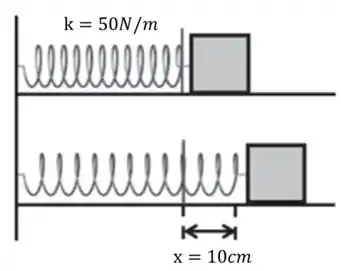
Agora, como calculamos a energia potencial elástica? Você não lembra? Então vem comigo!
A energia potencial elástica pode ser calculada dessa forma aqui
Em que o é a constante elástica da mola e é o deslocamento dela a partir da posição de equilíbrio.
Passo 2
E os dados do enunciado foram:
Percebeu onde mora o problema? Exato, a unidade do deslocamento não está em metros, ela está em centímetros. Então precisamos passar para metros antes de aplicar na fórmula!
É bem simples, passar de centímetros para metros é só dividir por :
Pronto, já podemos aplicar na fórmula!
Passo 3
Substituindo essas informações na fórmula
Temos:
Vamos começar a resolver pela potência:
Então:
Multiplicando no numerador:
Substituindo novamente:
Agora só resta fazer a divisão:
Essa é a nossa resposta final!