O eixo de um ventilador gira com a velocidade igual a . O motor elétrico impõe um torque de . Calcule a potência de giro desse eixo.
Passo 1
O motor tem que aplicar uma força ao eixo para fazer ele girar. Ou seja, o motor deve dar energia ao eixo através dessa força. Por causa disso, dizemos que o motor realiza trabalho no eixo.
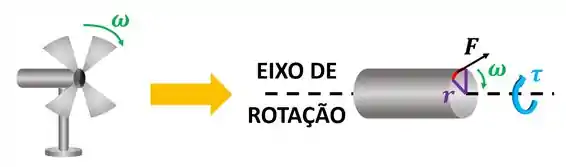
A taxa de energia que esse motor entrega ao eixo por unidade de tempo é chamada de potência. A fórmula de potência para o eixo girando é dada por:
onde:
- é a potência de giro do eixo. Ela é a incógnita do problema. Sua unidade no Sistema Internacional (S.I.) é o watt ;
- é o torque aplicado ao eixo. Sua unidade em S.I. é o newton-metro . Ele é dado pelo enunciado.
- é a velocidade angular de giro do eixo. Sua unidade é o radiano por segundo . Seu valor foi informado pela questão.
Então, para achar a potência precisamos substituir os dados na equação. Vamos deixar isso pro próximo passo.
Passo 2
Substituindo os valores na fórmula, temos:
Achamos o resultado final!
Resposta
Exercícios de Livros Relacionados
86- Considere o automóvel e a resistência de rolamento descritos no Prob. 4.27 . Qual é a velocidade do automóvel quando a motor está fornecendo potência igual a 30H P ?
90- Uma resistência elétrica de 15Ω é alimentada com uma corrente de 10A . Determine a potência dissipada na resistência
5 Dois conjuntos cilindro-pistão estão conectados através de uma tubulação de modo que as pressões nos conjuntos podem ser consideradas iguais. O cilindro do conjunto 1 apresenta diâmetro D1 e aquele
6 As cabeças dos pistões dos motores Diesel não são planas e isto é feito para melhorar as condições de combustão na câmara do motor. A forma da cabeça do pistão influencia o trabalho realizado pelos
14 Um reboque de trator que se move a 60 km/h, é movido por uma força com módulo igual a 1,2 kN. Qual é a potência associada a este movimento?