Um tanque rígido de contém de , de ar e de hélio separados por dois pistões móveis. Os êmbolos estão inicialmente travados por pinos. Nesta condição, o ocupa do tanque e o ocupa . Considere que os três gases perfeitos possuem de temperatura. Além disso, suponha que a massa molar do vale , que a massa molar do ar vale e que a massa molar do vale . Após a remoção dos pinos, os pistões se movimentam. As temperaturas de todos os gases permanecem constantes durante toda a movimentação. Após os pistões pararem, determine se cada gás realizou ou sofreu trabalho durante o reposicionamento dos êmbolos.
Passo 1
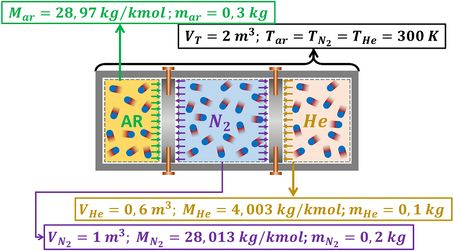
O enunciado pede para que a gente determine se o trabalho é realizado por cada gás ou se ele é realizado sobre cada gás. Mas antes de resolver isso, vamos listar os dados fornecidos pelo enunciado com uma figura para organizar os pensamentos.
Como podemos descobrir se o gás realiza ou sofre trabalho? Observando a variação de volume dos gases depois que os pinos são removidos! Por exemplo, se o volume ocupado pelo ar aumenta, o ar realiza trabalho . Se ele diminui, o ar sofre trabalho.
onde é o volume do ar antes de removerem os pinos e é o volume ocupado pelo ar depois de removerem os pinos.
Essa regra de variação de volume serve para os outros dois gases também!
Os volumes e foram dados pelo enunciado.
O volume foi fornecido de forma indireta pelo enunciado, quando ele disse o volume total do tanque rígido .
Mas como podemos determinar os volumes de cada gás depois do pino ser removido e os pistões se equilibrarem em uma nova posição?
Dividimos essa tarefa em três etapas:
- Achar as pressões dos gases antes das travas dos pistões serem removidas através das fórmulas de gás perfeito;
- Achar as pressões dos gases depois das travas dos pistões serem removidas através das fórmulas de gás perfeito, lembrando que as temperaturas dos gases não variam;
- Achar os volumes ocupados pelos gases depois da remoção das travas .
Ufa! Quanta coisa! É muita coisa mesmo! Mas resolver o problema em etapas vai facilitar o entendimento.
No próximo passo vamos descobrir como calcular as pressões iniciais de cada gás!
Passo 2
As pressões dos gases, de quando os pinos ainda não tinham sido removidos, são dadas indiretamente pelo problema. Para calculá-las, precisamos reorganizar a fórmula de gás perfeito. Para o ar, temos que:
é encontrado pela fórmula:
A pressão do nitrogênio é obtida da mesma forma.
O é encontrado pela fórmula:
Por fim, a pressão do hélio é encontrada pela mesma equação.
O é encontrado pela fórmula:
Agora que já sabemos calcular as pressões iniciais, vamos calcular as pressões finais .
Passo 3
Existem três informações escondidas no enunciado. Elas são fundamentais para o cálculo das pressões finais! A primeira é que essas pressões finais são todas iguais.
Essa informação está implícita na questão, quando o enunciado diz que os pistões param. Se eles param quer dizer que todas as pressões se equilibrar e fazem a mesma força nos êmbolos.
Também precisamos lembrar que as massas, assim como as temperaturas, permanecem iguais durante o movimento dos pistões.
Por último, devemos lembrar que o volume do tanque rígido não varia. Ou seja, a soma de todos os volumes finais ocupados pelos gases continua sendo igual a .
Com essas informações, somos capazes de desenvolver as fórmulas das pressões finais. A primeira etapa é usar a informação de que as temperaturas permanecem constantes durante o movimento dos pistões. Se isso é verdade, temos que:
Se esses valores são constantes, os valores finais e iniciais são iguais.
Reorganizando essas equações, já encontramos uma fórmula para .
No entanto, ainda não conhecemos as pressões finais. Só sabemos que elas são iguais. De qualquer forma, podemos usar essa igualdade para achar uma nova expressão para os volumes finais.
Usando essas fórmulas na equação da soma dos volumes, achamos que:
Reorganizando a equação, descobrimos que:
Pronto, achamos as pressões finais! Além disso, podemos usar esse valor de para encontrar os volumes finais nas fórmulas acima!
Então vamos começar a fazer os cálculos pra chegar nos volumes finais!
Passo 4
A primeira etapa é calcular , e .
Sabendo disso, pulamos para o cálculo do volume ocupado pelo ar, antes das travas do pistão serem removidas.
Com esses resultados, substituímos os valores nas fórmulas de pressão inicial.
Com as pressões iniciais, descobrimos a pressão final de todos os gases.
Por fim, conseguimos achar os volumes finais, substituindo as pressões finais nas fórmulas.
Com esses valores, decobrimos que: o volume do ar aumentou, o volume do hélio aumentou e o volume do diminuiu. Isso significa que o ar realizou trabalho, o hélio realizou trabalho e o nitrogênio sofreu trabalho!
Resposta
O ar realizou trabalho, o hélio realizou trabalho e o nitrogênio sofreu trabalho!