Uma célula de concentração é formada por dois pares redox idênticos, no catodo e no anodo, em diferentes concentrações de íons nos respectivos compartimentos. Calcule o potencial gerado pelas seguintes células de concentração.
a) Uma barra de mergulhada numa solução contendo de em contato elétrico com outra barra de , mergulhada numa solução contendo de .
b) Um metal inerte, como a platina (), mergulhada numa solução ácida de , em contato elétrico com outro eletrodo de platina, mergulhado numa solução ácida de . Ambas soluções contem sob pressão de 1 bar. Dica:
Passo 1
Primeiro de tudo e antes de mais nada, vamos entender essa história aí de pilha de concentração.
Antes da gente ver a equação do seu Nersnt, pra formar a pilha nós precisávamos de dois materiais com potenciais diferentes. Essa “ddp” entre eles justificava o funcionamento da pilha galvânica.
Agora, a gente já é gente grande da eletroquímica, e já tá ligado que diferenças nas concentrações alteram os potenciais das pilhas.
Uma consequência disso, é que podemos formar pilhas de concentração, onde temos um só metal nos dois eletrodos. Pra que a pilha funcione, usamos concentrações diferentes nas soluções de cada semi-célula.
Pra esses casos, o potencial da pilha é calculado por:
Antes de ficar quebrando cabeça, vamos ver como usamos isso na prática!
Passo 2
a) Em pilhas com diferentes eletrodos, nós calculamos o e, depois, transformamos em pela equação de Nersnt.
No entanto, numa pilha de concentração, a reação global é totalmente “zerada”. Olha só, no caso do cobre se oxidando no anodo e se reduzindo no catodo:
A global seria:
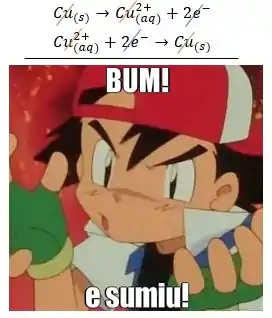
Tudo foi “cortado”.
Pra evitar esse problema, aplicamos Nersnt nas semirreações, e não na reação global!
Passo 3
Primeiro vamos descobrir em qual compartimento teremos a oxidação: o de menor concentração ou o de maior concentração de ?
Reação normal:
Aplicando Nersnt nessa reação:
O nosso produto da reação, não é um íon! É o ! Como ele não está em fase aquosa, a gente usa na fórmula.
Para a célula de menor concentração de íon:
Para a célula de maior concentração de íon:
O que a gente descobre com isso?
Quem tem MAIOR POTENCIAL DE REDUÇÃO vai SOFRER REDUÇÃO.
O que nossos cálculos aí de cima mostraram é que na célula com MAIOR concentração, temos o MAIOR POTENCIAL DE REDUÇÃO.
Conclusão:
Isso sempre acontece ok? Em célula de concentração o anodo vai ser o de menor concentração.
Beleza?
Então, pro nosso exercício aqui:
E a diferença de potencial da célula será:
Pra usar a outra fórmula:
A representação da reação global da pilha pode ser feita assim:
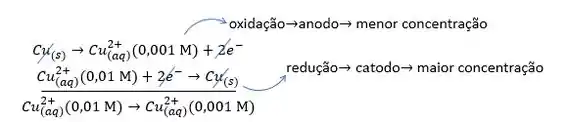
Atenção: os potenciais que calculamos com a equação de Nersnt são de redução porque nossa baseamos na reação de redução e no potencial de redução!
Passo 4
b) Parece complicado, mas é a mesma coisa.
A platina não entra no jogo, afinal ele é inerte.
Temos uma pilha de concentração, onde no catodo teremos a seguinte reação:
E no anodo:
Então precisamos saber onde teremos o catodo e onde teremos o anodo.
Para :
Para p:
Como e já sabemos que na semi-célula de menor concentração teremos o anodo, podemos dizer que:
Sendo a reação global:
Passo 5
Em pilhas de concentração, então, precisamos aplicar Nersnt em cada semi-célula pra descobrir seus potenciais fora das condições normais.
Dada a reação de redução:
Pra concentração de M:
Pra concentração de M:
Confirmando o que já sabíamos: na semi-célula com M temos menor potencial de redução, portanto ocorrerá a oxidação e ela será o anodo.
O potencial da pilha será, então:
Você pode, claro, inverter a reação do anodo no sentido de oxidação e fazer as contas com o potencial de oxidação.
Também podemos usar a reação global, olha só:
A matemática e a química são duas lindas né? Não importa o caminho, importa chegarmos lá!
Resposta
a)
b)