Determinar os valores da permeabilidade e do fator a partir dos dados experimentais obtidos por permeametria.
Meio de areia artificialmente consolidado com de araldite.
- Granulometria da areia:
- Fluido: água
- Comprimento do meio:
- Área da seção de escoamento:
- Porosidade do meio:
- Dados de velocidade superficial e queda de pressão:
![]()
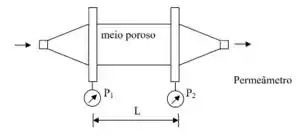
Passo 1
O enunciado nos deu dados experimentais de e pediu pra calcularmos COM BASE NOS DADOS EXPERIMENTAIS os valores de (permeabilidade) e (fator sem nome).
Como vamos ter que usar os dados experimentais, temos que partir da equação do movimento para relacionar e ; esse desenvolvimento eu já fiz pra você lá na teoria, então vou pular, ok? Só temos que identificar qual caso aplicar.
Já que o fluido é água, podemos assumir fluido incompressível; e como o enunciado NÃO fala que o escoamento é lento, NÃO podemos assumir isso e, por isso, usamos a equação de Forchheimer para . Daí vale:
Depois de identificado o caso, é só fazer regressão linear com os dados:
Temos que nos atentar se estamos usando tudo no mesmo sistema de unidades; vou adotar o CGS, daí vou converter logo e . No caso do , vou primeiro chegar numa expressão geral pra conversão e depois converto todos.
Daí, em :
![]()
Ah! Na teoria, eu defini e, dessa forma, fica positivo. Nessa questão, ele definiu de forma que ficava negativa e por isso colocou um menos na tabela, pra deixar positivo; então definiu . Daí o da tabela original é o mesmo que o meu .
Passo 2
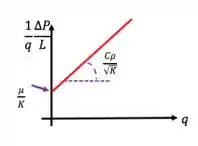
Agora é só fazer a regressão linear com os dados fornecidos; comparando a equação de trabalho com a equação de uma reta:
Temos que:
Adicionando uma linha para na nossa tabela e usando :

Fazendo a regressão linear :
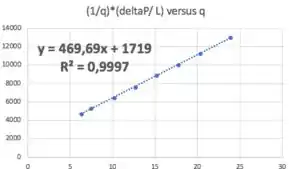
Daí:
Na primeira equação não conhecemos duas variáveis; na segunda, uma. Então começamos pela segunda.
Da primeira:
Repara que nem usamos algumas informações.