Determinar os valores da permeabilidade e do fator a partir dos dados experimentais obtidos por permeametria.
Meio não consolidado de areia
- Granulometria da areia:
- Fluido: ar a e pressão atmosférica na descarga
- Comprimento do meio:
- Área da seção de escoamento:
- Porosidade do meio:
- Dados de velocidade mássica e queda de pressão:
![]()
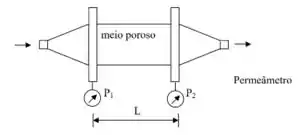
Passo 1
O enunciado nos deu dados experimentais de e pediu pra calcularmos COM BASE NOS DADOS EXPERIMENTAIS os valores de (permeabilidade) e (fator sem nome).
Como vamos ter que usar os dados experimentais, temos que partir da equação do movimento para relacionar e ; esse desenvolvimento eu já fiz pra você lá na teoria, então vou pular, ok? Só temos que identificar qual caso aplicar.
Como o fluido é ar, o fluido é compressível; e como o enunciado NÃO fala que o escoamento é lento, NÃO podemos assumir isso e, por isso, usamos a equação de Forchheimer para . Daí vale:
Depois de identificado o caso, é só fazer regressão linear com os dados:
Temos que nos atentar se estamos usando tudo no mesmo sistema de unidades; vou adotar o CGS; cuidado com a unidade desse aí porque ela pode confundir. Embora tenha um na unidade, NÃO está no CGS; pra pressão, a unidade do CGS é . Daí vou converter logo ; vou primeiro chegar numa expressão geral pra conversão e depois converto todos.
![]()
Massss, para fluido compressível, não basta saber o ; como temos que calcular , já que ele aparece na fórmula a se fazer regressão linear, e a fórmula dele é:
Precisamos de . O segundo já foi dado, só precisamos passar pro CGS:
Já , como:
Calculando em cada ponto:

Passo 2
Antes de fazermos a regressão linear, precisamos calcular para cada caso.
Para calcular ,precisamos da temperatura em escala absoluta; vou passa-la pra Kelvin.
Como estamos trabalhando no CGS, usamos:
Por se tratar de ar atmosférico, . Daí:

Passo 3
Agora que temos tudo que precisamos, podemos fazer a regressão linear:
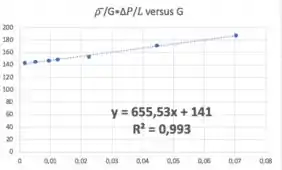
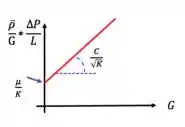
Comparando a equação de trabalho com a equação de uma reta, :
Daí:
Antes de continuarmos, precisamos do . Indo atrás de algum valor tabelado, achamos que para o ar nas condições do problema, . Daí:
Da outra equação: