Circuitos Térmicos
Teoria
A ideia dos circuitos térmicos é utilizá-los pra resolver sistemas mais complexos, onde temos várias resistências. Essas resistências podem estar em série ou em paralelo.
Você se lembra de circuitos elétricos, ou já faz muito tempo que você não vê isso?
O princípio vai ser justamente o mesmo que usamos pra circuitos elétricos!
Resistências em Série
Quando trabalhamos com isso em circuitos elétricos, vimos que, quando temos resistências em série, a resistência equivalente era igual à soma de todas essas resistências.
Pois bem, para resistências térmicas em série, a resistência térmica total será a soma de todas as resistências térmicas.
Dá uma olhada na parede composta aqui embaixo! Ela tem 3 camadas de diferentes materiais, e ainda tem convecção nas superfícies.
O calor, ao fluir da esquerda para a direita, será obrigado a passar tanto pelas convecções, quanto pelos materiais. No final das contas, a gente tem um conjunto de resistências (de convecção e condução) em série.
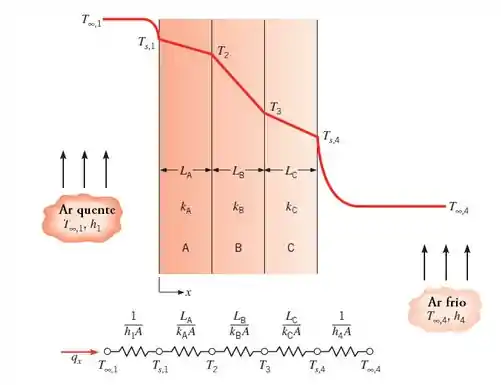
Então, a resistência total equivalente do circuito é dada por:
Resistências em Paralelo
A analogia com resistências elétricas em paralelo continua válida!
Agora, o inverso da resistência térmica total será a soma dos inversos das resistências térmicas em paralelo.
Vamos dar uma olhada nessa situação agora:
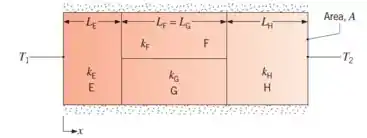
Repare que, se o calor flui no sentido positivo de , após passar pelo material , parte do calor flui pelo material , enquanto a outra parte flui pelo material , somando-se ao passar pelo material .
Sendo assim, o circuito térmico que representa esse sistema é:
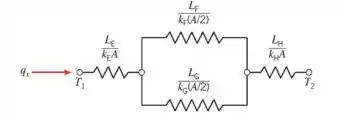
Para a parte que está em paralelo (no centro), a gente tem o seguinte:
Então, a resistência total equivalente do circuito completo (em série e em paralelo) é dada por:
Resistência Térmica de Contato
Muitos problemas que envolvem circuitos térmicos dizem no enunciado para você considerar o “contato perfeito” entre as superfícies, e muitos nem falam nada, já partindo do princípio que vamos considerar isso.
Mas o que isso quer dizer?!
Na realidade, o contato imperfeito entre as superfícies resulta em uma queda de temperatura entre as interfaces dos materiais. A ideia é mais ou menos a seguinte: quando olhamos de longe duas superfícies em contato, parece que elas estão perfeitamente em contato, certo?
Mas se olharmos um pouco mais de perto, vamos ver que não é bem assim que as coisas acontecem.
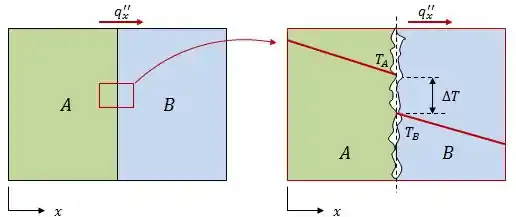
Esse contato imperfeito ocorre por conta da rugosidade dos materiais. Dessa forma, nós definimos a Resistência Térmica de Contato da seguinte forma:
Então é importante ficar esperto pra ver se o problema quer ou não que você considere a resistência de contato.
Show de bola! Já podemos quebrar a cabeça com os exercícios.
Resistências em Paralelo
Resistência Térmica de Contato
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Em um processo de fabricação, um filme transparente está sendo fixado a um substrato, conforme mostrado no esquema. Para curar a fixação a uma temperatura , uma fonte radiante é utilizada para fornecer um fluxo de calor (), que é totalmente absorvido pela superfície fixada. A parte posterior do substrato é mantida a enquanto a superfície livre do filme é exposta ao ar a e um coeficiente de transferência de calor por convecção .
Mostre o circuito térmico representando a situação de transferência de calor em regime estacionário. Identifique todos os elementos, nós e as taxas de calor. Deixe na forma simbólica.
Considere as seguintes condições: , e . Calcule o fluxo de calor necessário para manter a superfície fixada a .
Passo 1
Mostre o circuito térmico representando a situação de transferência de calor em regime estacionário. Identifique todos os elementos, nós e as taxas de calor. Deixe na forma simbólica.
Pra montar um circuito térmico, temos antes que identificar as temperaturas em cada superfície e quais as resistências que existem entre elas: se é de condução, de convecção ou de radiação.
A situação ilustrada pode ser esquematizada da seguinte maneira:
Então, já identificamos quais são as temperaturas do sistema e conseguimos ver que parte do calor é transferido por condução através do substrato () para a parte de baixo e parte dele é transferido para cima, primeiro por condução no filme () e depois por convecção () para o meio fluido.
Dessa forma, ficamos com o seguinte circuito térmico:
Em que:
- representa a resistência térmica por convecção em .
- representa a resistência térmica por condução no filme em .
- representa a resistência térmica por condução no substrato em .
Passo 2
Considere as seguintes condições: , e . Calcule o fluxo de calor necessário para manter a superfície fixada a .
Agora, bora resolver o problema de verdade, usando os dados fornecidos pelo enunciado. Antes de tudo, a gente tem que calcular cada uma das resistências térmicas:
Note que estamos calculando as resistências a partir do fluxo e por isso a área do filme e do substrato não entram na fórmula.
Como o fluxo de calor de até passa por duas resistências, a gente pode calcular a resistência térmica equivalente () desse trecho e, como essas resistências estão em série, basta somar uma com a outra:
Analisando o circuito, a gente pode ver que parte da energia que entra () sai por cima () e parte dela sai por baixo (). Então, podemos escrever que:
Escrevendo os fluxos em função das resistências:
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptada) Considere uma camada da pele humana exposta para a atmosfera ao redor. Considere uma camada de tecido gorduroso que possua de espessura e cuja superfície interna seja mantida a uma temperatura de . Em um dia calmo, o coeficiente de tranferência de calor por convecção na supeffíce externa é de , mas com ventos de ele cheg a . Em ambos os casos, a temperatura do ar ambiente é de .
Dado: .
Qual é a razão entre as perdas de calor (por unidade de área da pele) em um dia calmo e em um dia de vento?
Qual será a temperatura da superfície externa da pele em um dia calmo? E em um dia de vento?
Qual a temperatura que o ar deveria ter no dia calmo para causar a mesma perda de calor que ocorre com a temperatura do ar no dia em que há vento?
Passo 1
A situação do enunciado pode ser esquematizada da seguinte forma:
Vendo o esquema, você consegue prever qual o sentido do fluxo de calor? A temperatura interna da pele () é maior do que a temperatura do ar (), então a gente espera que o fluxo saia da pele para o ar!
Essa energia térmica é transferida por dois mecanismos: primeiro por condução na pele e depois por convecção para o ar. Beleza! Como existem dois mecanismos de transferência em série, seria legal representarmos o circuito térmico. Então, se liga aí:
No circuito, a gente já consegue identificar quais são as temperaturas de cada superfície (interna e externa) e a temperatura do fluido (ar), além das resistências de condução e de convecção.
O enunciado pede a relação entre as perdas de calor por unidade de área da pele, ou seja, isso é o que a gente chama de fluxo de calor (). Com base no circuito, a gente tem que:
Como as resistências estão em série, basta somarmos a resistência de condução com a de convecção:
Ótimo! A gente já sabe e e ainda podemos calcular a resistência por condução (). A única variável que a gente vai mudar de uma situação pra outra é a , porque ela depende do coeficiente de convecção ().
Passo 2
Qual é a razão entre as perdas de calor (por unidade de área da pele) em um dia calmo e em um dia de vento?
Então, a gente precisa calcular as resistências térmica de convecção () pro dia calmo e pro dia de vento.
A resistência de condução é dada por:
Logo:
- Para o dia calmo, a gente tem que:
Assim:
Com a resistência calculada, a gente pode calcular o fluxo de calor com:
Passo 3
- Para o dia de vento, a gente tem que:
- Para o dia calmo, a gente tem que:
- Para o dia de vento, a gente tem que:
Assim:
Com as resistência, o fluxo será:
Dess forma, a razão entre entre as perdas de calor (por unidade de área da pele) em um dia calmo e em um dia de vento () será:
Logo:
Isso quer dizer que a perda de calor num dia calmo equivale a da perda de calor observada em um dia de vento.
Isso condiz com o mecanismo físico, porque quanto maior a velocidade do fluido, mais fluido passa em uma região para roubar calor em cada intervalo de tempo, então maior é a convecção.
Passo 4
Qual será a temperatura da superfície externa da pele em um dia calmo? E em um dia de vento?
Bora lembrar do nosso esquema aqui embaixo:
Fazendo um balanço de energia na superfície externa da pele, a gente nota que:
Logo, a gente conclui que:
Em termos das resistências térmicas:
Então, a gente sabe que o fluxo de calor de condução é igual ao de convecção, que é igual ao fluxo total, porque a quantidade de energia témrica que passa pelo circuito em determinado tempo é a mesma!
Então, a gente pode escrever o seguinte:
Isso significa que, pra calcular a temperatura da superfície externa, a gente não precisa fazer no trecho todo, só em um dos trechos: no de condução ou de convecção.
Vou escolher aqui fazer na condução, porque ela não muda de uma situação pra outra, mas tanto faz, tá bem? Mas tanto faz! ^^
Isolando a temperatura da superfície externa (), temos que:
Substituindo os valores que calculamos na letra a), para o dia calmo, temos:
Passo 5
Isolando a temperatura da superfície externa (), temos que:
Substituindo os valores que calculamos na letra a), para o dia de vento, temos:
Passo 4
Qual a temperatura que o ar deveria ter no dia calmo para causar a mesma perda de calor que ocorre com a temperatura do ar no dia em que há vento?
Bom, agora a gente tem comparar duas situações: o dia de vento com o ar a e o dia calmo com o ar a uma temperatura de . Em ambas as situações a pele continua com sua superfície a .
Então, bora calcular que temperatura faz com que a perda de calor no dia calmo seja igual a do dia com vento!
Já vimos que o fluxo de calor no dia de vento com a temperatura do ar a equivale a:
Então, igualando com a expressão para o fluxo no dia calmo, teremos:
Isolando a temperatura do ar , teremos:
Já calculamos a resistência térmica de condução e a de convecção para o dia calmo:
Dessa maneira, substituindo os valores:
Logo, a temperatura que o ar deveria ter no dia calmo para causar a mesma perda de calor que no dia em que há vento equivale a aproximadamente .
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
A parede composta de um forno consiste em três materiais, dois dos quais com condutividade térmica ( e ) e espessura ( e ) conhecidas. O terceiro material (), que se encontra entre os materiais e , possui espessura () conhecida, mas a condutividade térmica () é desconhecida.
Sob condições de operação em regime estacionário, medidas revelam uma temperatura na superfície externa do forno de , uma temperatura na superfície interna de e uma temperatura do ar interior do forno de . O coeficiente convectivo interno é conhecido, sendo igual a . Qual é o valor de ?
Passo 1
O primeiro passo na resolução dos exercícios é esboçar o circuito térmico, então mãos à obra:
O que queremos encontrar é o valor da condutividade térmica no material . Como o fluxo é constante ao longo de todo o circuito, a gente pode escrever o seguinte:
- O fluxo de calor no primeiro trecho do circuito (de a ) é dado por:
- O fluxo de calor no segundo trecho do circuito (de a ) é dado por:
Igualando as expressões de cada trecho, temos o seguinte:
Como a nossa incógnita é o e ele está dentro da expressão de , bora isolar esse termo:
Agora só nos resta calcular as resistências térmicas do lado direito da equação! ^^
Passo 2
Bora calcular cada uma das resistências então:
Substituindo na expressão que a gente achou, a gente fica com:
A resistência térmica de condução é dada por:
Então, temos que:
Assim, concluímos que:
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Uma casa tem uma parede composta de madeira, isolamento de fibra de vidro e placas de gesso, conforme indicado no esquema. Em um dia frio de inverno, os coeficientes de transferência de calor por convecção são e . A área total da superfície da parede é de . Admita que: , e .
Determine uma expressão que simbolize a resistência térmica total da parede, incluindo os efeitos da convecção interna e externa para as condições dadas.
Determine a perda total de calor através da parede.
Se o vento estivesse soprando violentamente, aumentando para , determine o percentual do aumento da perda de calor.
Qual a resistência que controla o fluxo de calor total através da parede?
Passo 1
Determine uma expressão que simbolize a resistência térmica total da parede, incluindo os efeitos da convecção interna e externa para as condições dadas.
A primeira coisa que temos que fazer é montar o circuito térmico, para identificar as temperaturas e resistências em cada trecho do sistema.
Então, temos que:
No circuito, a gente pode ver as resistências de convecção nas duas extremidades e as 3 resistências de condução, uma para cada material. Como todas as resistências estão em série, basta somarmos as expressões para simbolizar a resistência térmica total:
Ou podemos ainda representar a resistência térmica total sem unidade de área:
Passo 2
Determine a perda total de calor através da parede.
Agora temos que calcular a perda de calor através da parede composta. Então, precisamos calcular a taxa de calor que sai de dentro () para fora ():
Então, a gente precisa calcular a resistência térmica total (). Sabemos que:
Então:
Substituindo os valores do enunciado:
Então, a gente pode encontrar a resistência térmica total dividindo pela área:
Assim:
Agora a gente já pode calcular a taxa de calor:
Passo 3
Se o vento estivesse soprando violentamente, aumentando para , determine o percentual do aumento da perda de calor.
Se o coeficiente de convecção externo () mudar, a resistência total também vai alterar e assim teremos:
Assim:
A nova taxa de calor será dado por:
Passo 4
Podemos calcular a razão entre as taxas de calor () da seguinte forma:
Ou seja, a perda de calor na situação de ventos mais fortes é maior que a perda de calor nos dias mais calmos. Como a diferença foi tão pequena, mesmo aumentando o coeficiente externo , já sabemos que a resistência de convecção não é a mais relevante.
Passo 5
Qual a resistência que controla o fluxo de calor total através da parede?
Já vimos que a resistência de convecção não é a limitante, então bora verificar as resistências por condução:
Com isso, a gente consegue ver que a resistência limitante é referente à camada de fibra de vidro ().
Resposta
O circuito pode ser ilustrado da seguinte forma:
A perda de calor total equivale a: .
A perda de calor na situação de ventos mais fortes é 0,46 % maior.
A resistência que controla/limita a taxa de calor é a resistência térmica de condução no material B:
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Considere uma parede composta que inclui um painel lateral em madeira dura com de espessura; travessas de suporte em madeira dura com dimensões de por , afastadas com de distância (centro a centro) e com espaço livre preenchido com isolamento à base de fibra de vidro (revestida de papel, ); e uma camada de de painéis de gesso (vermiculita).
Qual é a resistência térmica associada a uma parede com de altura e de largura (possuindo 10 travessas de suporte, cada uma com de altura)?
Passo 1
A ideia aqui é a seguinte: como cada travessa está afastada centro a centro de , vamos considerar uma unidade da parede da seguinte forma:
Então vamos começar calculando a resistência térmica total dessa unidade, e a resistência térmica total será dada pela resistência em paralelo de unidades dessa (correspondente a 10 suportes).
Passo 2
Após passar pela madeira, parte do fluxo de calor flui pelo isolamento, e parte flui pela travessa de madeira. Dessa forma, o circuito térmico para esse sistema é dado por:
Então vamos começar calculando cada resistência térmica, beleza? Vamos numa batida só:
Passo 3
Para calcular a resistência térmica total dessa unidade, vamos começar calculando a resistência térmica em paralelo :
Dessa forma, a resistência térmica da unidade é dada por:
Passo 4
Show de bola! Mas a resistência que encontramos é a resistência de apenas uma unidade. A resistência térmica total será dada considerando um circuito em paralelo formado por 10 unidades dessa lado a lado, logo:
Resposta
Exercício Resolvido #6
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Duas placas em aço inoxidável, com espessura de , estão sujeitas a uma pressão de contato de sob vácuo. Nestas condições, há uma queda global de temperatura através das placas de .
Qual é o fluxo térmico através das placas?
Qual é a queda de temperatura no plano de contato?
Dado: e .
Passo 1
Qual é o fluxo térmico através das placas?
O fluxo térmico pode ser calculado através da resistência térmica total, dada por:
Então vamos começar calculando a resistência térmica total.
Nesse caso, o nosso circuito térmico é constituído por resistências térmicas em série, da seguinte forma:
Dessa forma, a resistência térmica total será dada por:
Onde:
Substituindo os valores:
Passo 2
Agora estamos prontos pra calcular o fluxo térmico, que será dado por:
Onde , logo:
Passo 3
Qual é a queda de temperatura no plano de contato?
Agora que já sabemos o fluxo térmico, a queda de temperatura no plano de contato pode ser calculada através da resistência térmica de contato, dada por:
Substituindo os valores:
Resposta
Exercício Resolvido #7
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Considere uma parede plana composta constituída por dois materiais com condutividades térmicas e e espessuras e . A resistência térmica de contato na interface entre os materiais é conhecida, sendo .
O material está em contato com um fluido a com e o material está em contato com um fluido a , no qual .
Qual é a taxa de transferência de calor através de uma parede que tem de altura e de largura?
Esboce a distribuição de temperaturas.
Passo 1
Qual é a taxa de transferência de calor através de uma parede que tem de altura e de largura?
O circuito térmico nesse caso será constituído por resistências térmicas em série, onde o calor é transferido do material (que está em contato com o fluido a maior temperatura) para o material (que está em contato com o fluido a menor temperatura).
Dessa forma:
Opa! Conhecemos e . Para calcular a taxa de transferência de calor , podemos usar a resistência térmica total desse circuito da seguinte forma:
Então partiu calcular a resistência térmica total.
Passo 2
Como todas as resistências térmicas estão em série, temos que:
Onde:
Substituindo os valores:
Passo 3
Agora estamos prontos pra calcular a taxa de transferência de calor:
Onde:
Substituindo os valores:
Passo 4
Esboce a distribuição de temperaturas.
Olhando novamente para o nosso circuito térmico:
O nosso trabalho agora é determinar as temperaturas , , e . Então vamos fazer isso tudo num embalo só, beleza?
Dessa forma, a distribuição de temperatura terá essa cara:
Resposta
Exercício Resolvido #8
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptada) Aproximadamente componentes elétricos discretos podem ser colocados em um único circuito integrado (chip), com uma dissipação térmica na ordem de . O chip, que é muito fino, tem a sua superfície externa exposta a um líquido dielétrico com e , e a sua superfície interna está conectada à placa de circuito.
A resistência térmica de contato entre o chip e a placa é de , e a espessura e a condutividade térmica da placa são e , respectivamente. A outra superfície da placa está exposta ao ar ambiente, no qual e .
Esboce o circuito térmico equivalente para condições de regime estacionário. Usando as variáveis, identifique as resistências apropriadas, as temperaturas e os fluxos térmicos.
Sob condições de regime estacionário nas quais um fluxo térmico dissipado no chip é , qual é a temperatura do chip?
Passo 1
Esboce o circuito térmico equivalente para condições de regime estacionário. Usando as variáveis, identifique as resistências apropriadas, as temperaturas e os fluxos térmicos.
O circuito térmico é caracterizado por resistências térmicas em série, onde temos um fluxo de calor sendo adicionado circuito pelo chip e fluxos de calor e sendo retirados do circuito pelas convecções realizadas pelo ar e pelo refrigerante.
Dessa forma, o circuito térmico vai ter essa cara:
Passo 2
Sob condições de regime estacionário nas quais um fluxo térmico dissipado no chip é , qual é a temperatura do chip?
Fazendo o balanço de energia, vemos que:
Para calcular vamos considerar todas as resistências térmicas à esquerda do chip, e para calcular vamos considerar todas as resistências térmicas à direita do chip.
Dessa forma, teremos o seguinte:
Onde:
Substituindo os valores:
Agora é só arrumar a bagunça:
Resposta
Exercício Resolvido #9
Questão 1, PUCRIO, P1-2003
Considere uma parede de um forno industrial, composta por 3 diferentes materiais e espessura total de . A espessura do material 1 é de e a dos materiais 2 e 3, é de .
A área total transversal vale , e os materiais 2 e 3 possuem áreas transversais iguais. A temperatura máxima admitida na superfície externa da parede é de .
A temperatura do gás no interior do forno vale , e o coeficiente convectivo interno de troca de calor vale .
Considere regime permanente e condução unidimensional, e obtenha:
O circuito térmico equivalente.
A temperatura na parede interna do forno .
A taxa de transferência de calor total através da parede.
Passo 1
O circuito térmico equivalente.
O circuito é determinado analisando o caminho do fluxo de calor. Assim, o mesmo passa do gás para a placa de material 1 e, em seguida, parte vai para o material 2 e parte vai para o material 3. Dessa forma, o circuito térmico equivalente terá a seguinte forma:
Passo 2
A temperatura na parede interna do forno .
Analisando somente a parede interna do forno, vemos que a quantidade de calor que entra, deve ser igual à quantidade de calor que sai. Assim:
Passo 3
Onde é a resistência térmica total de condução. A resistência equivalente entre as resistências térmicas em paralelo será:
A resistência térmica equivalente de condução será:
Passo 4
Assim, a temperatura interna do forno será:
Passo 5
A taxa de transferência de calor total através da parede.
A taxa de transferência de calor pode ser calculado da seguinte forma:
Onde é a resistência térmica total do circuito, dada por:
Assim:
Resposta
Exercício Resolvido #10
Questão 1, PUCRIO, Lista P1
(Adaptado) Uma parede plana é composta de quatro diferentes materiais, de acordo com a figura abaixo.
As condutividades térmicas são iguais a: ; ; ; . Encontre a taxa de transferência de calor, considerando que ele se propaga apenas em uma direção. Considere que os blocos b e c têm o mesmo tamanho.
Passo 1
Para calcular a taxa de transferência de calor, podemos usar a definição de resistência térmica. Nesse caso, o fluxo de calor entra pela placa , depois se divide entre as placas e , e flui através da placa .
Dessa forma, teremos o seguinte circuito térmico:
De forma que a taxa de transferência será dada por:
Passo 2
Pra calcular a resistência térmica equivalente, vamos começar calculando a resistência equivalente das resistências em paralelo. Assim:
A resistência térmica do circuito será:
Passo 3
A taxa de transferência de calor será:
Resposta
Exercício Resolvido #11
Questão 2, UFF, P1-2016/2
Um compensado especial é composto por 100 folhas. Desse conjunto de folhas, a metade é composto por um material cuja a condutividade térmica é de e com de espessura e a outra metade é composto por um material de condutividade térmica de e de espessura.
O compensado é formado por essas folhas de forma intercaladas.
Uma amostra desse material foi disposta para análise experimental, visando determinar a condutividade térmica equivalente em cada uma das direções da amostra cuja as dimensões planares são de .
Determine, justificando sua resposta matematicamente, qual é a condutividade térmica que deveria ser encontrada pelas metodologias experimentais, supondo que não há resistência de contato entre as folhas.
Assumindo que a determinação experimental da condutividade térmica na direção perpendicular a folha foi 10% menor que a teoricamente prevista acima (para a mesma direção), calcule qual é a resistência de contato média que supostamente existe entre cada folha.
Passo 1
O compensado pode ser pensado como um circuito térmico com 100 resistências térmicas em série.
Onde:
Passo 2
A resistência térmica equivalente será dada por:
Substituindo os valores:
A condutividade equivalente do circuito será:
Passo 3
Se o experimento encontrou uma condutividade térmica menor, a resistência térmica de condução equivalente será dada por:
Sendo assim, a resistência de contato total no circuito térmico é dada por:
Substituindo os valores:
Como temos 100 folhas, haverá 99 superfícies de contato. Dessa forma, a resistência de contato entre cada folha será:
Resposta
Exercício Resolvido #12
Questão 1, UFF, P1-2017.1
(Adaptado) Em uma casa muito distante, uma parede foi construída, composta de camadas de madeira (face externa a casa), isolamento à base de fibra de vidro e placa de gesso (face interna da casa). Em um dia frio de inverno a temperatura no exterior é de e os coeficientes de película internos e externos são e .
A área total da parede é de . Sabendo que a camada de madeira possui de espessura, a fibra de vidro possui originalmente de espessura e a placa de gesso possui de espessura.
Determine, nessas condições, qual a quantidade de calor trocada com o ambiente, sabendo que a temperatura interna será de .
Qual a espessura que a placa de fibra de vidro deve ter para diminuir em 50% a troca térmica?
Passo 1
Determine, nessas condições, qual a quantidade de calor trocada com o ambiente, sabendo que a temperatura interna será de .
A taxa de transferência de calor será dada por:
Onde é a resistência térmica total do sistema, dada por:
Onde o índice corresponde à região interna, o índice corresponde ao gesso, o índice corresponde à fibra de vidro, o índice corresponde à madeira, e corresponde à região externa.
Assim:
De acordo com a tabela A.3 do Incropera:
Substituindo os valores:
Passo 2
Qual a espessura que a placa de fibra de vidro deve ter para diminuir em 50% a troca térmica?
Agora, queremos descobrir para que seja igual a (metade do valor que encontramos na letra ).
Do passo anterior, temos que:
Reorganizando a equação acima pra isolar o , teremos o seguinte:
Substituindo os valores:
Resposta
Exercício Resolvido #13
Questão 3, UFF, P1-2016.1
(Adaptado) Avalie a transferência de calor do ar exterior para um ambiente interno através de uma parede dupla com um espaço de ar entre as duas paredes.
Na situação analisada, as paredes são concreto seco com altura de , largura de e espessura de de cada uma das paredes. O espaço de ar entre as duas paredes tem espessura de de tal forma que o ar confinado nesse espaço não entra em movimento.
Sabendo-se que a temperatura do ar externo é de e que o coeficiente de película para convecção e de e a temperatura do ar no interior do ambiente é de com coeficiente de película , determine a taxa de transferência de calor do ar exterior para o ar no interior do ambiente nos seguinte cenários:
Assumindo que NÃO há radiação de calor no espaço confinado.
Assumindo que o espaço entre as duas paredes foi reduzido a zero.
Assumindo que há radiação de calor no espaço confinado e essa tem uma taxa de .
Considere a condutividade térmica do ar igual a .
Passo 1
Assumindo que NÃO há radiação de calor no espaço confinado.
A situação pode ser resumida de acordo com o seguinte:
Onde a taxa de transferência de calor será dada por:
Onde a resistência térmica do circuito é dada por:
Passo 2
Substituindo os valores, onde:
Assim:
Assim, a taxa de transferência de calor será:
Passo 3
Assumindo que o espaço entre as duas paredes foi reduzido a zero.
Nesse caso, o circuito térmico irá ser composto da seguinte forma:
Logo, a resistência térmica equivalente será:
Substituindo os valores:
Assim, a taxa de transferência de calor será:
Passo 4
Assumindo que há radiação de calor no espaço confinado e essa tem uma taxa de .
Como o calor está sendo transferido do ar externo para o ar interno, a temperatura da parede externa será maior que . Dessa forma, podemos escrever o circuito térmico da seguinte forma:
Assim, a taxa de transferência de calor do ar externo para o ar interno será:
Onde é o valor que encontramos na letra , e o fluxo térmico de radiação é dado por:
Dessa forma:
Resposta
Exercício Resolvido #14
Questão 2, UFRJ, P1-2008.1
O fundo de uma panela de alumínio tem de espessura.
Com a finalidade de aumentar a taxa de transferência de calor, propõe-se um novo projeto para o fundo da panela que consiste de uma camada de cobre , com de espessura, inserida entre duas camadas de alumínio de de espessura.
O contato entre as camadas é perfeito. Você recomendaria este novo projeto ao dono da fábrica de panelas? Justifique sua resposta.
Passo 1
A taxa de transferência de calor irá aumentar se a resistência térmica do sistema diminuir. Inicialmente, com o sistema sendo composto somente pelo alumínio, a resistência térmica era dada por:
Passo 2
Com o novo sistema, a resistência térmica do sistema passa a ser dada por:
Onde o índice 1 se refere à camada de alumínio e o índice 2 se refere à camada de cobre.
Como a resistência térmica está aumentando, a taxa de transferência de calor será reduzida. Logo, o projeto não é recomendável.
Resposta
O projeto não é recomendável pois a taxa de transferência de calor irá diminuir.
Exercício Resolvido #15
Questão 1, UFRJ, P1-2007.1
A temperatura máxima a ser mantida na superfície interna de um forno de cozinha é de . A parede do forno é composta por duas placas de aço de de espessura, com isolante térmico entre elas. O contato entre o isolante e as placas é perfeito.
Dimensione a espessura de isolante necessária para que a temperatura externa do forno não exceda , sabendo que a temperatura da cozinha varia entre e e que o coeficiente de transferência de calor entre a superfície externa do forno e o ar é de .
Qual é a taxa de calor perdida através da parede do forno para as condições de seu projeto?
Passo 1
O circuito térmico correspondente ao sistema pode ser representado da seguinte forma:
Como já temos a temperatura da cozinha e da superfície externa forno, podemos calcular a taxa de transferência de calor da seguinte forma:
O problema nos disse que a temperatura da cozinha varia entre e . Então, como queremos também calcular a espessura de isolamento necessária, vamos considerar o pior cenário.
Olhando para a taxa de transferência através do isolante:
Vemos que, quanto menor a taxa de transferência de calor, maior será a espessura de isolamento necessária. Dessa forma, vamos considerar como pior caso a temperatura da cozinha igual a , que vai nos dar o menor valor da taxa de calor.
Dessa forma:
Passo 2
Como não temos as temperaturas e , para calcular a espessura de isolamento, vamos considerar a seguinte porção do circuito:
Dessa forma:
A resistência térmica equivalente dessa porção será:
Onde é dada por:
