Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 178
Ouro é comumente utilizado no empilhamento de semicondutores para formar interconexões que transportam sinais elétricos entre diferentes dispositivos no conjunto. Além de ser um bom condutor elétrico, interconexões de ouro são também efetivas na proteção dos dispositivos geradores de calor aos quais estão fixadas através da condução de energia térmica para fora dos dispositivos, para a vizinhança, regiões mais frias. Considere um filme fino de ouro que tem seção transversal de .
- Para a imposição de uma diferença de temperaturas de , determine a energia conduzida ao longo de uma interconexão (filme fino) com de comprimento. Avalie as propriedades a .
- Represente graficamente as condutividades térmicas longitudinal (na direção do ) e na menor dimensão (direção mais fina) do filme de ouro como funções da espessura do filme , na faixa .
Passo 1
Fala aí! Pronto para mais uma questão? Vamos nessa!
Nosso enunciado nos conta algumas características do ouro, sendo usado como semicondutor… E ele nos dá duas letrinhas para resolver, na letra a quer que a gente calcule a energia ao longo do filme fino de ouro, já a letra b, quer que a gente faça um gráfico com as condutividades térmicas…
Vamos anotar nossos dados do enunciado:
Mas vamos precisar de um dado adicional… A condutividade do ouro na temperatura de , podemos encontrar na tabela A.1 do livro… Ela será:
Bom, partiu então!
Passo 2
Começando pela letra a, vamos usar a lei de Fourier para calcular o que ele pediu!
Ops! Mas não temos o nosso , e agora?
Relaxa! Sabemos encontrar ele:
Show! Então vamos substituir isso na nossa equaçãozinha:
ou
Show! Partiu letra b!
Passo 3
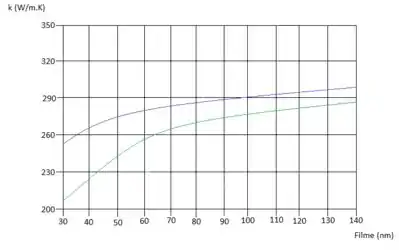
Vamos agora representar graficamente a nossa condutividade térmica ao longo do eixo , que é dada por:
Vamos ter então apresentar nosso gráfico, sendo a curva azul correspondendo ao e a verde ao …
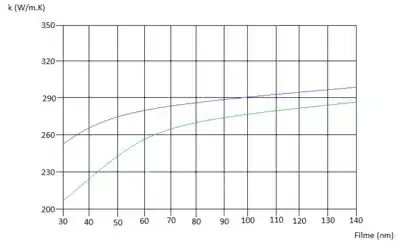
Uhul! Arrasamos!
Resposta
- .
