Condução em Sistemas Radiais
Produzido por Giovanna RonzéTeoria
Introdução
Fala, galerinha! Tudo certo? Prontos pra desbravar novos mares? Então, bora lá!
Nesse tópico, a gente vai ver basicamente como tratar da condução em geometrias com curvas.

Ahaha É isso mesmo, vamos ver aqui basicamente dois tipos de parede: as cilíndricas e as esféricas.
A gente já estudou a condução em paredes planas, então vocês vão tirar de letra isso daqui, é bem parecido com o que já vimos: a gente vai trabalhar com circuitos térmicos, determinar taxas e temperaturas. Vem comigo então!
Equação do Calor para Sistemas Cilíndricos
No tópico de balanço de energia, a gente já viu a Equação do Calor para coordenadas cartesianas (, e ). Mas a gente também pode fazer o mesmo esquema num corpo cilíndrico e obter a Equação do Calor em coordenadas cilíndricas (, e ).
Fazendo o balanço de energia num elemento infinitesimal, como o mostrado aqui embaixo, a gente vai obter a Equação do Calor, dada por:
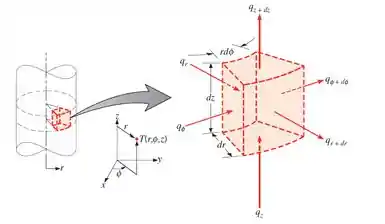
Em boa parte dos problemas, nós tratamos de situações com as seguintes características:
- Condução unidimensional em : não há variação em ou .
- Estado estacionário: não há variação ao longo do tempo.
- Sem geração de energia: o termo é nulo.
- Propriedades constantes: a condutividade térmica pode sair da derivada.
Dessa forma, podemos simplificar a Equação do Calor para:
Bora resolver juntos essa equação, sigam-me os bons:
Integrando a equação em termos do raio , a gente fica com:
Reorganizando a equação:
Integrando novamente a equação em termos do raio :
Como a gente tem que determinar as duas constantes, a gente precisa de duas condições de contorno. No caso mais simples de sabermos as temperaturas das superfícies, ficamos com:
Utilizando essas condições para encontrar e , chegaremos a essa expressão final da temperatura:
Pronto! Essa é a distribuição de temperatura em uma casca cilíndrica!
Resistência Térmica para Sistemas Cilíndricos
Pela definição de Resistência Térmica, temos que:
Para encontrar a taxa transferência de calor por condução ao longo do raio, basta a gente usar a equação de Fourier:
Derivando a expressão de que achamos, a gente fica com:
Para achar a taxa, basta a gente multiplicar pela área de troca térmica :
Logo:
Assim, a gente conclui que a resistência de condução para superfícies cilíndricas é dada por:
Importante: Note que a taxa não depende do raio, mas o fluxo depende! Então, a gente só pode usar circuito térmico tratando de taxa e nunca tratando de fluxo!!
Show! Agora vamos usar o mesmo princípio para sistemas esféricos!
Equação do Calor para Sistemas Esféricos
Agora você já sacou como funciona! Em coordenadas esféricas (, e ), a equação fica a seguinte:
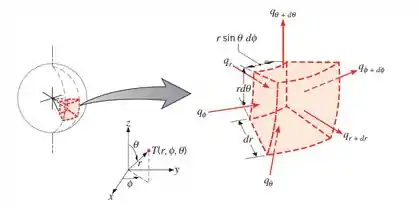
Talvez a sua reação ao ver essa equação tenha sido essa (pelo menos a minha foi):

Sim, eu sei, ela assusta demais! Mas, fazendo as mesmas considerações que fizemos para a equação em coordenadas esféricas e resolvendo a Equação do Calor para encontrar a temperatura, a gente fica com:
Vamos tratar aqui de uma casca de raio interno e raio externo .
Utilizando as mesmas condições de contorno de temperaturas conhecidas na superfície:
Resistência Térmica para Sistemas Esféricos
O fluxo de calor, pela equação de Fourier ao longo de será:
Multiplicando pela área de troca térmica , a gente fica com:
Logo:
Assim, a gente conclui que a resistência de condução para superfícies esféricas é dada por:
Se liga! Não se preocupe se você se assustou um pouco com as equações, o quadro abaixo resume o que há de mais importante aqui. Nos problemas, geralmente a boa é lembrar da Equação do Calor e da Resistência Térmica de Condução. O resto a gente é brabo e consegue descobrir, se necessário.

Agora que você já está equipado com todo esse arsenal de expressões pra calcular resistências térmicas e taxas, você já pode ir à guerra! ^^
Resistência Térmica para Sistemas Cilíndricos
Equação do Calor para Sistemas Esféricos
Resistência Térmica para Sistemas Esféricos
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Uma parede cilíndrica é composta de dois materiais de condutividades térmicas e que são separados por um aquecedor elétrico delgado, para o qual as resistências de contato na interface são desprezíveis.
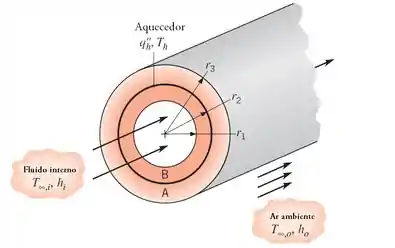
O líquido bombeado através do tubo encontra-se a uma temperatura e fornece um coeficiente de convecção na superfície interna da composição. A superfície externa é exposta ao ar ambiente, que está a e fornece um coeficiente de convecção . Em condições de regime estacionário, um fluxo de calor uniforme é dissipado pelo aquecedor.
Esboce o circuito térmico equivalente do sistema e expresse todas as resistências em termos das variáveis relevantes.
Obtenha uma expressão que pode ser utilizada para determinar a temperatura do aquecedor ().
Obtenha uma expressão para a razão entre os fluxos de calor para os fluidos interno () e externo (). Como as variáveis do problema podem ser ajustadas para minimizar essa razão?
Passo 1
Esboce o circuito térmico equivalente do sistema e expresse todas as resistências em termos das variáveis relevantes.
Como a gente já tá acostumado, bora fazer o circuito térmico. Para os sistemas radiais (cilindros e esferas), a gente só precisa fazer o circuito do centro pra fora, porque é simétrico pro outro lado!
Identificando as temperaturas em cada superfície (nós do circuito) e desenhando as resistências entre elas, a gente fica com:
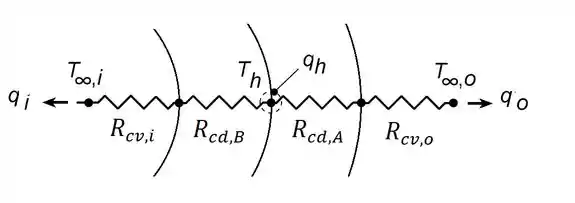
Como sabemos, as expressões de resistência térmica de convecção são as mesmas no caso de placa plana, cilindros ou esferas, o que muda é o cálculo da área de troca térmica ().
Para o caso acima, teremos:
Expressando as áreas em termos dos raios, temos que:
Mas a gente não conhece o comprimento do cilindro, e agora? Nem precisa, a gente pode simplesmente expressar as resistências relativas ao comprimento do cilindro:
“Show! Mas e as resistências de condução?” Ah, essas daí são diferentes do caso da parede plana e também diferem dos casos da esfera. Para corpos cilíndricos, a gente viu que:
Então, escrevendo as resistências térmicas de condução nas cascas cilíndricas e , a gente fica com:
Pela mesma estratégia que fizemos com as resistências de convecção, ficamos com:
Agora a gente já pode desenhar o circuito com as respectivas resistências em termos dos parâmetros relevantes do problema:

Passo 2
Obtenha uma expressão que pode ser utilizada para determinar a temperatura do aquecedor ().
Agora a gente precisa calcular a temperatura do aquecedor. Para isso, a gente pode tentar fazer o balanço de energia no ponto referente ao aquecedor!
Pelo circuito a gente pode ver que uma certa energia entra pelo ponto aquecedor e que ela vai se dissipar por dois caminhos diferentes ( e ). Como o enunciado dá os fluxos de saída por unidade de comprimento, para igualar entrada e saída precisamos multiplicar pelo perímetro do cilindro .
Sendo assim:
OBS: Se você achar essa forma muito complicada, você pode fazer o balanço na forma de taxa de calor (e não por fluxo), daí você vai ver que o comprimento vai cancelar em todos os termos da equação!
Continuando com a equação, a gente pode substituir as expressões dos calores:
Agora é álgebra, acabou a Transferência de Calor! A gente só tem que isolar a temperatura da equação. Então, bora lá!
Colocando a temperatura em evidência, a gente fica com:
E finalmente:
Passo 3
Obtenha uma expressão para a razão entre os fluxos de calor para os fluidos interno () e externo (). Como as variáveis do problema podem ser ajustadas para minimizar essa razão?
A razão entre os calores () é dada por:
Substituindo as expressões de e de , a gente fica com:
Para minimizar essa razão, a gente precisa diminuir os termos do numerador e/ou aumentar aqueles do denominador. De maneira, prática podemos:
- Aquecer o fluido que passa pelo interior (aumenta )
- Resfriar o fluido que passa pelo interior (diminui )
- Aumentar a velocidade do fluido no interior (aumenta )
- Aumentar a espessura da casca cilíndrica (aumenta )
- Diminuir a espessura da casca cilíndrica B (diminui )
Entre outras modificações quanto aos materiais e os fluidos.
Resposta

E as possíveis modificações para diminuir seu valor são listadas abaixo:
- Aquecer o fluido que passa pelo interior (aumenta )
- Resfriar o fluido que passa pelo interior (diminui )
- Aumentar a velocidade do fluido no interior (aumenta )
- Aumentar a espessura da casca cilíndrica (aumenta )
- Diminuir a espessura da casca cilíndrica B (diminui )
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Uma casca esférica composta, com raio interno é construída de chumbo () de raio externo e aço inoxidável () de raio externo . A cavidade é preenchida com resíduos radioativos que geram calor a uma taxa de . Propõe-se que o recipiente seja submerso em águas oceânicas que estão a uma temperatura e fornecem um coeficiente de convecção uniforme para a superfície externa do contêiner. Existe algum problema associado a essa proposta?
Admita que a temperatura de fusão dos materiais são: e .
Passo 1
Você deve ter se perguntado: “Como assim ‘algum problema associado à proposta’?” Então, muitas vezes em processos de transferência de calor, a gente tá interessado em saber se um sistema “aguenta” a quantidade de calor gerada, ou seja, se alguma peça vai derreter.
Sabendo disso, nosso objetivo nessa questão é calcular as temperaturas de cada superfície e garantir que elas não ultrapassem os pontos de fusão do respectivo material.

Agora que sabemos o que fazer, bora dar uma olhadinha num esquema da situação:
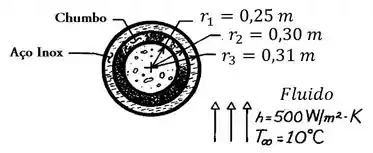
Como não há geração na casca esférica composta em si, a gente pode construir o circuito térmico representativo do sistema:
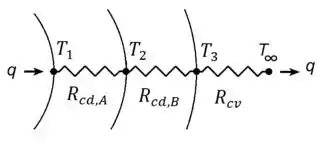
Em que as resistências de condução em geometrias esféricas têm uma expressão diferente da placa plana e das geometrias cilíndricas:
Passo 2
Pelo circuito, a gente pode escrever que:
A gente viu que a fonte calor desse sistema são os resíduos radioativos no interior da cavidade, que geram uma taxa volumétrica de .
Então, para achar a taxa de calor que flui pela esfera até o ambiente, basta a gente multiplicar pelo volume da cavidade:
Dessa forma:
Passo 3
Então, só nos resta calcular as resistências no circuito térmico que fizemos!
Para a condução no chumbo:
Para a condução no aço inoxidável:
Calculando ainda a resistência de convecção:
Passo 4
Substituindo na expressão da taxa, teremos:
Isolando a temperatura da superfície , a gente fica com:
Passo 5
Como é a temperatura na superfície do chumbo e seu valor é menor que o da temperatura de fusão desse material (), então o chumbo não vai derreter ali.
Mas e as demais temperaturas ( e )? Temos que calculá-las pra saber se os materiais vão derreter? Não! “Mas por quê?”
Note que é a maior temperatura do sistema, pois ela é a temperatura da superfície mais próxima da região onde a energia é gerada. Então:
Se o chumbo não derrete na maior temperatura do sistema (), então ele também não derreterá na superfície mais externa (a temperatura de ).
E o aço? A temperatura de fusão do aço é de (ou ), que é bem maior que e, consequentemente, também será maior que e . Logo, ele também não derreterá!
Resposta
Não há nenhum problema associado ao derretimento das peças utilizadas no sistema.
Nenhuma temperatura das superfícies supera os pontos de fusão do aço e do chumbo!
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
(Adaptada) Um tubo de aço de paredes finas com de diâmetro é utilizado para transportar vapor saturado a uma pressão de através de um ambiente onde a temperatura do ar é e o coeficiente de convecção na superfície externa do tubo é . A resistência convectiva do lado vapor pode ser desprezível.
Qual é a perda de calor por unidade de comprimento para o tubo sem isolamento? A emissividade do aço pode ser considerada .
Encontre a equação que descreve a temperatura da superfície externa do isolamento em função dos parâmetros conhecidos (polinômio de quarto grau) se uma camada de isolamento térmico ( e ) com de espessura for aplicada ao redor do tubo.
Após resolver o polinômio de quarto grau, você achou uma temperatura de . Estime a perda de calor com o isolamento.
Passo 1
Qual é a perda de calor por unidade de comprimento para o tubo sem isolamento? A emissividade do aço pode ser considerada .
Sem o isolamento, a gente tem a situação simples de uma casca cilíndrica envolvida por um grande ambiente e que sofre convecção externa. Esquematizando, fica mais ou menos assim:
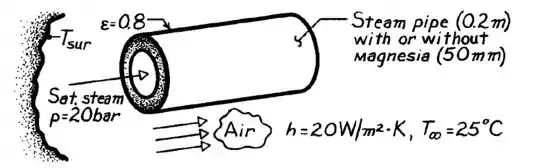
Como o enunciado diz que o vapor é saturado, com a pressão que foi dada podemos achar sua temperatura em uma tabela de propriedades da água saturada, encontrando .
Considerando então que a resistência de convecção interna é desprezível, a gente pode assumir que a temperatura da superfície interna da casca cilíndrica é igual à temperatura do vapor.
E, como a parede do tubo é fina, também desprezamos a resistência por condução, logo a temperatura da superfície externa também equivale a .
Bora fazer um balanço de energia na superfície do tubo, que é onde a energia é dissipada pro ambiente:
Em que a perda de calor é dada pela soma dos calores de convecção e radiação. Ou seja, calcular a perda de calor equivale a calcular quanto entra de calor na superfície ().
Bora calcular cada uma das taxas! Para a taxa de convecção:
Escrevendo em termos da taxa por unidade de comprimento, a gente fica com:
Para a taxa de radiação:
Assim como fizemos antes:
OBS: Você também pode escrever as taxas em função das resistências, mas, se você lembrar, a expressão da resistência de radiação é bem feiosa. Então, geralmente quando trabalhamos com radiação, é mais fácil usar direto a expressão das taxas.
Dessa maneira, a gente pode já substituir as taxas encontradas:
Passo 2
Encontre a equação que descreve a temperatura da superfície externa do isolamento em função dos parâmetros conhecidos (polinômio de quarto grau) se uma camada de isolamento térmico ( e ) com de espessura for aplicada ao redor do tubo.
Se aplicarmos uma camada de isolante em volta da casca cilíndrica, estaremos adicionando uma resistência de condução no sistema, como mostrado abaixo:
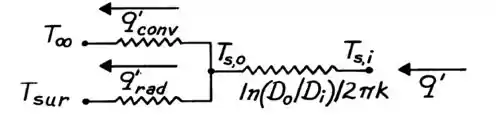
Como a gente não conhece as temperaturas, precisamos encontrar alguma delas pra poder calcular a taxa!
Ao fazermos o balanço de energia na superfície mais externa (que agora é a superfície externa do isolamento), teremos o seguinte:
Substituindo as expressões para a resistência térmica em paredes cilíndricas () e a área de troca térmica ()
Pronto! Note que a equação acima é um polinômio de quarto grau em e que todos os outros parâmetros dela são conhecidos!
Passo 3
Sabendo que a temperatura da superfície externa do isolamento equivale a , a gente pode calcular a taxa de calor de condução, pois ela representa a mesma quantidade de energia que é perdida pelo tubo por convecção e radiação.
Temos que:
A resistência de condução na parede cilíndrica pode ser calculada por:
Então:
Substituindo na expressão da taxa de calor:
Como não sabemos o comprimento do tubo, a gente pode simplesmente determinar a taxa de calor por unidade de comprimento ():
Logo, a perda de calor também será:
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
(Adaptada) Um tanque esférico para armazenar oxigênio líquido no ônibus espacial deve ser construído em aço inoxidável () com de diâmetro e de espessura de parede. O ponto de ebulição e o calor latente de fusão do oxigênio líquido são e respectivamente. O tanque será instalado em um grande compartimento cuja temperatura deve ser mantida a . Projete um sistema de isolamento térmico capaz de manter as perdas de oxigênio por evaporação abaixo de . Admita que a condutividade do isolamento equivale a e considere a resistência de convecção desprezível frente às demais resistências térmicas.
Passo 1
Nosso objetivo nessa questão é projetar um sistema de isolamento para uma esfera, isso significa que a gente tem que determinar qual a espessura do isolamento vamos usar pra revestir o tanque esférico.
A situação pode ser esquematizada da seguinte forma:
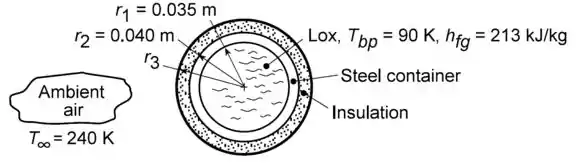
O sistema de isolamento deve ser tal que a taxa de evaporação do oxigênio líquido seja inferior a . “Mas o que isso tem a ver?”
A gente sabe que dada uma pressão fixa, a gente pode evaporar líquido fornecendo uma certa quantidade de energia, certo?
Então, a gente consegue relacionar a taxa de evaporação com a taxa de calor do sistema, dá uma olhadinha:
Essa é a equação do calor latente (), ou seja, a quantidade de energia pra evaporar a substância. Ele é função da quantidade de massa que evapora () e do calor latente de ebulição da substância em questão ().
Só que aqui a gente tá trabalhando com taxa, então bora dividir os dois lados da equação por :
Assim a gente fica com a taxa de calor () e com a taxa mássica de evaporação ():
Beleza! Então, se a gente precisa projetar um isolamento pra que a taxa de evaporação seja menor que , é a mesma coisa que projetar o isolamento pra uma taxa de calor menor que:
Beleza, agora já ficou um pouco melhor! O enunciado passa a ser “Projete um sistema de isolamento térmico para que a taxa de calor seja menor que ”.
Passo 2
Agora, a gente tem que calcular qual a espessura de isolamento que permite a passagem de somente . Bora lá!
A gente pode construir um circuito térmico considerando as paredes de aço () e de isolamento () mais a resistência de convecção externa ():
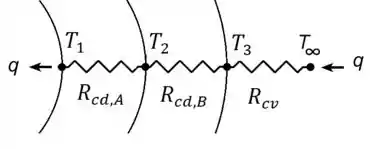
A gente pode escrever a equação para a taxa da seguinte maneira:
Note que, projetar a espessura de isolamento é o mesmo que determinar o valor de !
Bora encontrar o valor da resistência total primeiro:
Passo 3
Como as resistências estão em série, podemos escrever a resistência total como:
Mas, pelo enunciado, a gente pode desprezar a resistência de convecção, então:
Em que as resistências são dadas por:
Bora calcular a resistência do aço:
Passo 4
Beleza, então a gente pode escrever que:
Substituindo o que calculamos:
Viu que a resistência de condução é tão baixinha que não fez nem cócegas na resistência total? Pois é!
Abrindo a expressão da resistência de condução no isolamento, a gente fica com:
Logo:
Dessa forma:
Passo 5
Isso significa que a espessura de isolamento é dada por:
Ou seja:
Resposta
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 5ed.
Uma corrente elétrica de flui através de um cabo de aço inoxidável de diâmetro e resistência elétrica de (ou seja, por metro de comprimento de cabo). O cabo encontra-se em um ambiente que está a uma temperatura de , e o coeficiente total de transferência de calor, associado à convecção entre o cabo e o ambiente, é de aproximadamente .
Se o cabo estiver desencapado, qual será a temperatura em sua superfície?
Se um revestimento delgado for aplicado sobre o cabo, com uma resistência térmica de contato de , quais serão as temperaturas das superfícies do isolamento e do cabo?
Há preocupação em relação à capacidade do isolamento em suportar temperaturas elevadas. Qual a espessura do isolamento () que produzirá o menor valor para a temperatura máxima na camada de isolamento? Qual será o valor da temperatura máxima quando essa espessura de isolamento for utilizada?
Passo 1
Se o cabo estiver desencapado, qual será a temperatura em sua superfície?
Nosso primeiro desafio é o mais simples: a gente tem que calcular a temperatura no fio sem isolamento algum, ou seja, é só um corpo cilíndrico com geração de calor!
Como passa uma corrente elétrica pelo fio, a gente já sabe que vai gerar energia térmica () pelo efeito Joule. Então, bora escrever a expressão do fluxo de calor:
O enunciado não nos deu a informação quanto à resistência elétrica () do fio, mas sim a resistência por unidade de comprimento do fio (). Então, a gente pode escrever a taxa de calor gerada em termos do comprimento também:
Ou a gente pode fazer tudo em termos de taxa de calor, que depois o comprimento vai cortar! Essa é sempre uma boa estratégia, então vamos fazer isso!
Escrevendo em termos da taxa:
Passo 2
Com a taxa de calor já calculada, bora fazer um balanço de energia na superfície do fio:
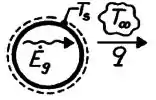
Então, conseguimos perceber que a energia gerada no volume do cilindro () entra na superfície externa e ela é dissipada por convecção.
Dessa maneira, a gente fica com o seguinte balanço de energia na superfície:
Fazendo um circuito térmico simples, temos:
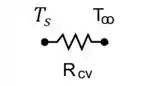
Substituindo a expressão da taxa por convecção (), a gente fica com:
Como a gente quer determinar a temperatura da superfície, bora isolar o termo :
Com a expressão da resistência , teremos:
Substituindo os valores do enunciado, a gente fica com:
Viu como cortou o comprimento do fio! ^^ Agora é só fazer os cálculos e:
Passo 3
Se um revestimento delgado for aplicado sobre o cabo, com uma resistência térmica de contato de , quais serão as temperaturas das superfícies do isolamento e do cabo?
Na nova situação, a gente vai pegar aquele mesmo fio da letra a) e vamos colocar um isolamento envolvendo sua superfície.
Daí você poderia pensar que ao colocar o isolamento, a gente iria ficar com um circuito térmico da seguinte maneira:
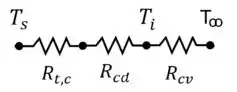
Tá certo! Mas aqui, o isolamento é delgado, ou seja, ele é muito, muito, muito fino!
Como a gente sabe, quanto menor a espessura do material, menor será a resistência térmica dele. Então, para um isolamento delgado, a resistência por condução dele será desprezível, ficando, então, só a contribuição da resistência de contato!
Sendo assim, o circuito adequado seria:
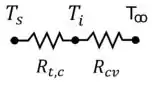
Fazendo novamente o balanço de energia na superfície do fio, a gente fica com uma expressão parecida com a que achamos na letra a):
Mas agora existe uma resistência térmica de contato em série com a de convecção!
Isolando a temperatura da superfície do fio, a gente fica com:
Mas cuidado!! A gente não pode colocar direto aquele valor de resistência térmica de contato do enunciado! Aquele valor é a resistência por unidade de área ()! Pra gente converter um no outro, basta dividir pela área de troca térmica:
Assim:
Substituindo os valores do enunciado:
Dessa maneira, a temperatura da superfície do fio será:
Passo 4
Ainda temos que calcular a temperatura da superfície do isolamento. Então, ao invés de pegar todo o circuito, bora pegar só a parte da convecção!
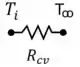
Assim, nossa equação vai ficar:
Isolando a temperatura do isolamento, ficamos com:
Substituindo os valores:
Hm, tá lembrado desse número!? Pois é, foi o mesmo valor que a gente achou na letra a). E já era de se esperar, porque estamos calculando a temperatura de um cilindro exposto ao mesmo fluido, com a mesma temperatura e com a mesma taxa de energia gerada.
Mas isso, claro, só porque o isolamento é delgado. “Mas e se ele não fosse?”. É isso que vamos ver na letra c), pequeno gafanhoto! Bora lá!
Passo 5
Há preocupação em relação à capacidade do isolamento em suportar temperaturas elevadas. Qual a espessura do isolamento () que produzirá o menor valor para a temperatura máxima na camada de isolamento? Qual será o valor da temperatura máxima quando essa espessura de isolamento for utilizada?
Agora sim! Aquele circuito térmico com a resistência de condução do isolamento vai aparecer aqui! Se liga aí:
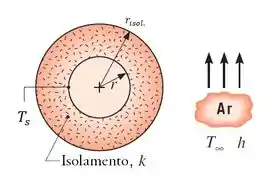
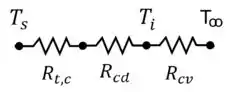
Então, a gente pode fazer o mesmo esquema que fizemos nas letras a) e b). Então, ao balanço de energia e além...
Agora, a gente tem a resistência de condução em série com as resistências de contato e de convecção! Isolando a temperatura da superfície do fio:
Com as expressões da resistência, ficamos com:
Mas agora temos um pequeno desafio: a gente não sabe nem a temperatura da superfície (), nem a espessura do isolamento (), pra poder calcular a resistência de condução. O que fazer?
Passo 6
O enunciado nos pediu uma coisa: a espessura do isolamento que produzirá o menor valor para a temperatura máxima na camada de isolamento.
Você já aprendeu no cálculo como encontrar máximo e mínimos, não é mesmo? Pois é, então aqui a gente pode achar qual é o valor de que faz a derivada de zerar!
Derivando a expressão que achamos em função de , teremos:
No ponto de mínimo, a derivada é nula:
Assim:
Ou seja, o raio do isolamento equivale a:
Assim, a espessura do isolamento será:
Passo 7
Agora que já descobrimos a espessura do isolamento, podemos determinar as temperaturas da superfície do fio e do isolamento.
Pela expressão que achamos da temperatura na superfície do fio:
Pelos cálculos, ficamos com:
Essa será a temperatura máxima do Sistema, dado que ela se refere a superfície mais próxima à geração de calor (que ocorre no interior do fio).
Resposta
Exercício Resolvido #6
Questão 1, PUCRIO, P1-2005
Um reservatório esférico armazena um gás a temperatura de . A parede do reservatório é composta de aço e tem uma espessura igual a .
Deseja-se adicionar um material isolante, de forma a reduzir a perda de calor do reservatório em . Determine a espessura necessária de isolante, considerando que a sua condutividade térmica vale . Considere o coeficiente de troca de calor interno igual a , e o externo igual a , e temperatura ambiente de .
Passo 1
Antes de colocar o isolante, o circuito térmico é dado por:
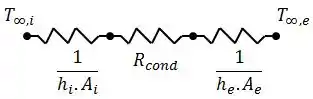
Onde:
Assim, a taxa de transferência de calor sem o isolante é dada por:
Onde a resistência térmica é dada por:
Trocando pela área da superfície da esfera () e substituindo os valores que temos:
Assim, a taxa de transferência de calor sem o isolante é dada por:
Passo 2
Ao colocar o isolante, a taxa de transferência de calor será a metade, logo:
Agora, como o isolante é colocado sobre a superfície externa da esfera, a resistência térmica equivalente será dada por:
Repare que:
Logo:
Assim, o raio externo do isolante será:
Passo 3
Assim, a espessura do isolante será:
Resposta
Exercício Resolvido #7
Questão 2, PUCRIO, Lista P1
(Adaptado) Um tanque esférico de m de diâmetro contém gás de petróleo liquefeito a . Um isolante de condutividade térmica igual a e espessura de é utilizado para reduzir o ganho de calor pelo gás.
Determine a posição radial na camada do isolante na qual a temperatura atinge , considerando que a temperatura ambiente vale e o coeficiente convectivo de troca de calor externo vale .
Passo 1
Como queremos descobrir em que ponto a temperatura será , podemos calcular esse ponto usando as resistências térmicas, onde o circuito térmico é dado por:
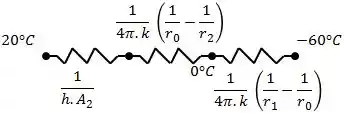
Onde é o raio que estamos procurando e está entre e .
Assim, podemos calcular o mesmo da seguinte forma:
Passo 2
Substituindo os valores, teremos:
![]()
Resposta
Exercício Resolvido #8
Questão 1, UFF, P1-2015.1
Uma semiesfera (uma esfera cortada pela metade) que estava com uma temperatura inicial teve sua face plana colocada sobre uma placa mantida a temperatura e esse conjunto foi colocado em um meio fluido a uma temperatura que é menor que .
Esse meio fluido está a uma velocidade bem caracterizada de tal forma que existe um coeficiente de película médio, , muito bem definido.
Partindo da equação geral de transferência de calor, equacione o modelo o modelo do perfil de temperatura da semiesfera e modele também a condições de contorno e iniciais. Utilize o sistema de coordenadas mais conveniente para a resolução do problema.
Justifique cada simplificação. Seja sucinto. NÃO RESOLVA A EQUAÇÃO, APENAS MODELE.
Passo 1
Como estamos trabalhando com uma semiesfera, vamos partir da equação de calor para sistemas esféricos, dada por:
Como temos uma condição em que a temperatura no plano da semiesfera é constante, a temperatura do sistema irá depender do raio e do ângulo . Dessa forma, podemos rescrever a equação acima da seguinte forma:
Supondo que não há geração de energia:
Supondo que as propriedades da semiesfera não dependam da temperatura:
Dividindo toda a equação por :
Passo 2
Vamos trabalhar agora com as condições de contorno e condição inicial do sistema.
Inicialmente, toda a semiesfera estava a uma temperatura , logo:
Para condições de contorno, podemos assumir temperatura constante em , convecção na superfície, e temperatura constante em . Dessa forma, teremos o seguinte:
Resposta
Exercício Resolvido #9
Questão 1, UFF, P1-2016.2
Existe a possibilidade de que no caso de uma tubulação, aumente-se a espessura de um certo isolante e isso aumente a transferência de calor ao invés de diminuir, tal como seria desejado ao aumentar a espessura de qualquer isolante. Isso nunca acontece quando a geometria é uma placa plana.
Explique o porquê, justificando MATEMATICAMENTE a sua resposta.
Passo 1
Isso pode acontecer porque, embora o isolante acrescente uma resistência térmica proporcional à espessura do isolante, a área externa também aumenta, aumentando a transferência de calor por convecção com o ambiente.
Vamos utilizar as seguintes variáveis pra resolver o problema:
- : Taxa de transferência de calor;
- : Temperatura na superfície interna do isolante;
- : Temperatura do ambiente;
- : Resistência térmica do isolamento;
- : Resistência térmica de convecção;
- : Raio externo do isolante;
- : Raio da superfície interna do isolante;
- : Coeficiente convectivo entre o tubo e o ambiente;
- : Comprimento do tubo.
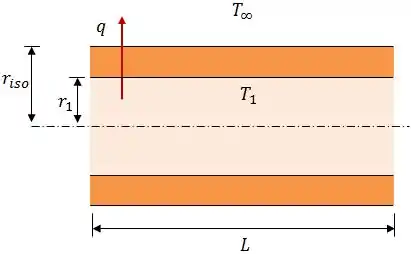
A taxa de transferência de calor pode ser escrita em função das resistências térmicas da seguinte forma:
Passo 2
Como estamos trabalhando com uma superfície cilíndrica, a resistência térmica de isolamento e a resistência térmica de convecção serão:
Assim, a taxa de transferência de calor será:
Supondo todos os parâmetros fixos, exceto o raio externo de isolamento , haverá um valor para o qual o isolamento deixará de reduzir a transferência de calor e vai passar a aumentar a transferência de calor.
Esse valor pode ser obtido se derivarmos a expressão da taxa de transferência de calor em relação a e igualarmos a zero.
Derivando a expressão de em relação a , teremos:
Analisando a expressão acima, veremos que ela será nula se:
Reorganizando a equação:
Esse será o raio crítico de isolamento.
![]()
Ou seja, caso , o isolante irá aumentar a transferência de calor. Mas se , o isolante irá reduzir a transferência de calor.
Resposta
Caso , o isolante irá aumentar a transferência de calor. Mas se , o isolante irá reduzir a transferência de calor.
Exercício Resolvido #10
Questão 6, UFRJ, P1-2007.1
Forneça a formulação matemática para o problema de condução de calor em um cilindro oco de raio interno , raio externo e altura , que encontra-se inicialmente na temperatura uniforme .
Uma das superfícies de topo do cilindro é aquecida por um fluxo de calor uniforme , enquanto a outra superfície de topo é isolada termicamente.
O cilindro troca calor internamente por convecção com um meio na temperatura , com coeficiente de transferência de calor . O cilindro troca calor através de sua superfície lateral externa com um meio na temperatura , com coeficiente de transferência de calor .
As temperaturas dos meios externo e interno, assim com os coeficientes de transferência de calor por convecção, são uniformes. Não há geração interna de energia no cilindro.
Passo 1
Como queremos fornecer a formulação matemática, precisamos obter uma equação a partir da equação de calor que, no caso de simetria cilíndrica, é dada por:
Com as informações fornecidas pelo problema, podemos fazer as seguintes considerações:
- Condução bidimensional nas direções radial e axial .
- Não há geração interna de energia.
- Propriedades constantes.
Assim, aplicando essas considerações à equação de calor, teremos:
Onde .
Passo 2
Para condição inicial, o problema nos disse que a temperatura é inicialmente uniforme e igual a . Dessa forma:
Passo 3
Para condições de contorno, como estamos trabalhando com condução bidimensional, teremos duas condições para a direção radial, e duas para a direção axial.
De acordo com o problema, uma das superfícies de topo do cilindro é aquecida por um fluxo de calor uniforme , enquanto a outra superfície de topo é isolada termicamente. Dessa forma, podemos dizer que:
Para as condições radiais, o problema nos disse que ambas as superfícies trocam calor por convecção, dessa forma:
Resposta
Exercício Resolvido #11
Questão 3, UFRJ, P1-2005.2
Um vaso esférico de aço inoxidável , com de diâmetro interno e de espessura de parede, é usado como reator químico.
A superfície externa do reator é resfriada por ar com temperatura de e coeficiente de transferência de calor de . No regime permanente, deseja-se saber.
Qual a taxa de calor transferida para o ar, sabendo-se que a temperatura da superfície interna do vaso e de ?
Qual a taxa volumétrica média de geração de energia no interior do reator?
Utilizando a taxa de geração de energia calculada no item e supondo que uma camada de de espessura de fibra-de-vidro seja usada para isolar o reator, responda qual é a temperatura da superfície interna do reator. O contato entre o isolante e parede do reator é suposto perfeito.
Passo 1
Qual a taxa de calor transferida para o ar, sabendo-se que a temperatura da superfície interna do vaso e de ?
Como temos as temperaturas do ar externo e da superfície interna do vaso, a taxa de transferência de calor pode ser calculada a partir do seguinte circuito térmico.
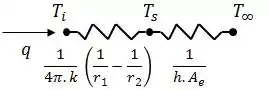
Onde . Assim, a taxa de calor será:
Substituindo os valores:
![]()
Passo 2
Qual a taxa volumétrica média de geração de energia no interior do reator?
A taxa de geração pode ser calculada da seguinte forma:
![]()
Passo 3
Utilizando a taxa de geração de energia calculada no item e supondo que uma camada de de espessura de fibra-de-vidro seja usada para isolar o reator, responda qual é a temperatura da superfície interna do reator. O contato entre o isolante e parede do reator é suposto perfeito.
Ao adicionar a camada de fibra de vidro, o circuito térmico passa a ser dado por:
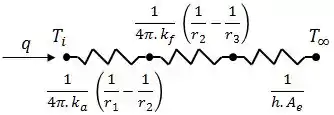
A resistência térmica total do circuito será dada por:
Como o problema nos pede pra usar a mesma taxa de geração de energia, ele na verdade está falando pra considerarmos a mesma taxa de calor que calculamos no item . Dessa forma, a temperatura da superfície interna será:
![]()
Resposta
Exercício Resolvido #12
Questão 2, UFRJ, P1-2004.2
Considere um fio elétrico longo com raio e condutividade térmica de . Por conta da corrente elétrica no fio, calor é gerado a uma taxa volum��trica uniforme .
O fio é revestido por um isolante elétrico cerâmico de de espessura, cuja condutividade térmica é de . A temperatura da superfície externa do isolante é .
Supondo propriedades termofísicas constantes e contato perfeito entre o fio e o isolante, no regime permanente, calcule:
Fluxo de calor na superfície externa do isolante elétrico;
Temperatura na interface entre o fio e o isolante;
Temperatura no centro do fio.
Passo 1
Fluxo de calor na superfície externa do isolante elétrico;
A taxa de transferência de calor pode ser calculada a partir do calor gerado no fio da seguinte forma:
O fluxo de calor será dado por:
Onde , sendo da espessura da camada de isolante.
![]()
Passo 2
Temperatura na interface entre o fio e o isolante;
Como já temos a taxa de transferência de calor e a temperatura na superfície externa do isolante, podemos calcular a temperatura na interface entre o fio e o isolante a partir do seguinte circuito térmico:
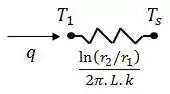
Assim:
Substituindo os valores:
![]()
Passo 3
Temperatura no centro do fio.
A taxa de calor no fio pode ser escrita como:
Substituindo os valores, teremos:
![]()
Resposta