Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 111
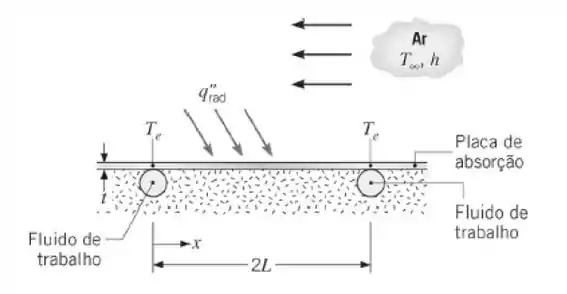
Tubos de cobre estão fixados a uma placa de um coletor solar, com espessura t, e o fluido de trabalho mantém a temperatura da placa acima dos tubos em Te. Há um fluxo térmico radiante líquido uniforme na superfície superior da placa, enquanto a superfície inferior encontra-se isolada termicamente. A superfície superior também está exposta a um fluido a , que fornece um coeficiente convectivo uniforme h.
- Deduza a equação diferencial que governa a distribuição de temperaturas T(x) na placa.
- Obtenha uma solução para a equação diferencial usando condições de contorno apropriadas.
Passo 1
Vamos que vamos galerinhaa??
Antes de qualquer coisa nós precisamos dar uma olhadinha mais de perto para o balanço de energia em um volume de controle diferencial, ok?
Então, se pegarmos um pedacinho da placa de comprimento :
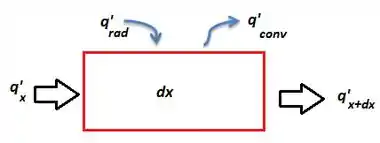
Quando nós fazemos o balanço de energia teremos que o calor sendo adicionado ao volume, e , e saindo do volume de controle, e , Então:
Agora nós precisamos achar cada um dos termos, ok?
A primeira coisa que devemos fazer aqui é escrever a equação de Fourier para a condução que ocorre a uma distância x:
E para uma distância
A transferência de calor por convecção pode ser dada como:
E a última que precisamos achar é a transferência de calor por radiação:
Agora nós podemos substituir tudo que temos:
Como o dx está presente em todos os termos:
E substituindo
Reescrevendo:
Então a equação diferencial que governa a distribuição de temperatura será dada por .
Bora seguir pra letra (b)??
Passo 2
Na letra (b) nós queremos uma solução para a equação diferencial usando condições de contorno apropriadas.
Se nós assumirmos que:
Então:
Na fórmula da letra (a):
Quando nós temos uma equação diferencial de segunda ordem com coeficientes constantes a solução é dada pela forma:
Onde:
Aplicando a primeira condição de contorno, quando e , então:
Se nós aplicarmos a segunda condição de contorno, quando e
Então nós precisamos derivar a solução que nós achamos, certo?
Igualando a zero e substituindo por
Substituindo na primeira equação do contorno o que acabamos de achar:
Isolando
Substituindo em
Colocando na solução:
Reorganizando:
Bem cabulosa, mas de um jeito legal !! Eu sei que vocês também gostaram !!