Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 108
Tubos de cobre estão fixados à placa absorvedora de um coletor solar plano, conforme mostrado na figura.
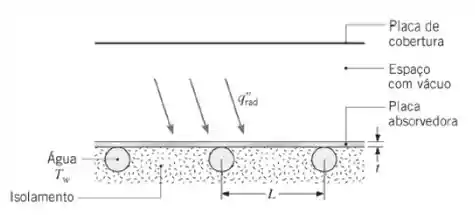
A placa absorvedora feita com a liga de alumínio (2024-T6) possui 6 mm de espessura e é isolada termicamente na sua superfície inferior. Há vácuo no espaço que separa a superfície superior da placa e a placa de cobertura transparente. Os tubos encontram-se espaçados entre si por uma distância L de 0,20 m e água escoa nos tubos para remover a energia coletada. A água pode ser suposta estar a uma temperatura uniforme = 60°C. Em condições de operação em regime estacionário, nas quais o fluxo radiante líquido na superfície absorvedora é de = 800 W/m², quais são a temperatura máxima na placa e a taxa de transferência de calor para a água por unidade de comprimento do tubo? Note que representa o efeito líquido da absorção da radiação solar pela placa absorvedora e da troca de radiação entre a placa absorvedora e a placa de cobertura. Você pode supor que a temperatura da placa absorvedora exatamente acima de um tubo seja igual à da água.
Passo 1
Tá legal! Vamos começar esse exercício aplicando o princípio da conservação de energia para um volume de controle diferencial na placa absorvedora, que vai de até , dessa forma, o calor que entra em mais a parcela que entra por será igual ao calor que sai em , então, podemos escrever:
No entanto, podemos escrever o calor em pelo princípio de Fourier, já que temos condução, então, teremos:
Podemos escrever agora a parcela de calor em como sendo o calor em mais a variação nesse trecho, então, teremos:
Então, substituindo as expressões encontradas na equação para o equilíbrio de energia, temos:
Simplificando essa expressão, conseguimos chegar em:
Passo 2
Agora nós vamos integrar a expressão obtida no passo 1 em , dessa forma, temos:
Integrando novamente em , chegamos em:
Agora precisamos encontrar o valor das constantes e . Para isso, vamos utilizar duas condições de contorno. A primeira delas é que não há gradiente de temperatura em , então, temos:
Substituindo esses valores na expressão encontrada, temos:
A outra condição de contorno é a temperatura da água que ocorre para , então, substituindo esses valores na equação para o perfil de temperatura, temos:
Então, o perfil de temperatura será:
Passo 3
A temperatura máxima ocorre exatamente no meio dos tubos, ou seja, em , dessa forma, substituindo esse valor de na expressão para o perfil de temperatura encontrada no passo 2, temos:
Para calcular a temperatura máxima, devemos buscar a condutividade térmica do alumínio na tabela A.1 do apêndice A, então, de lá, temos:
Então, substituindo os valores conhecidos na equação para a temperatura máxima, temos:
Agora, para encontrar a taxa de transferência de calor para a água por unidade de comprimento do tubo, como nós temos calor entrando por radiação, será todo esse calor. Só que como temos esse calor por unidade de área, e sabemos que o tubo dissipará calor por todo seu comprimento, temos que multiplicar o fluxo radiante absorvido pelo comprimento do tubo, então, temos: