Introdução ao escoamento em canais abertos
Produzido por Raphael EloiTeoria
Escoamento com superfície livre
Fala grande mestre!
Então aqui estamos de novo estudando escoamento em condutos. Mas agora tem uma diferença bem sútil mas com consequências muito fortes, comparado ao escoamento em condutos fechados:
Nossos escoamentos possuem superfície livre! Sim, todos querem liberdade, até as superfícies.
Os escoamentos mais comuns que existem na natureza são abertos, famosos rios:

Mas o ser humano que é malandro também resolveu usar isso pra resolver problemas da sua vida, é aí que calhas, rios retificados, etc que aparecem.

Beleza agora vamos começar a ver isso aí.
Boas notícias, lembra do diâmetro hidráulico ?
Tudo bem se não lembrar, eu te apresento de novo e a gente fala com o primo dele, o raio hidráulico :
O raio hidráulico que a gente vai usar não é nada menos que do diâmetro:
Esse , é a área da seção transversal do canal e o o perímetro MOLHADO. Isso é muito importante, o perímetro agora não é o da figura inteira pois existe a superfície livre!
Já adianto que tem muita coisa de escoamentos internos nesse tópico, então nada de falar mal da equação da energia, ela pode ficar chateada.
A parte boa é que como a pressão na superficie livre é igual em todos pontos, podemos reduzir a equação para os seguintes termos:
Beleza, mas isso de ter superfície livre complica algumas coisinhas também. Podem surigir ondas, aquele efeito de corredeira, cachoeira...
Então vamos delimitar os casos dos escoamentos que vamos estudar: serão escoamentos uniformes: com profundidade e declividade constantes. O desenho dos escoamentos fica tipo assim:
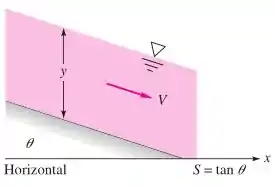
Fórmula de Chézy
Então até beleza?
Nos escoamentos que estudaremos a velocidade é constante, a profundidade é constante e a declividade é constante.
Logo nossa equação da energia fica só isso:
Vamos considerar que o escoamento é totalmente desenvolvido, logo como nos escoamentos internos a perda de carga continua naquela fórmula marota usando o diâmetro hidráulico:
No caso o vai depender de quanto do canal estamos estudando.Vale a pena pensar no , ou seja, distância final menos a inicial.
Se combinarmos as duas expressões a gente chega a conclusão de que a velocidade é igual :
Essa é a fórmula de Chézy. Esse fator é aquele famoso fator de atrito, só que agora com umas modificaçõezinhas:
Essa fórmula é mais ou menos a do Diagrama de Moody adaptada pro caso de canais abertos que são quase todos turbulentos e bem largos.
Um cara chamado Robert Manning quis simplificar um pouco as coisas e criou a seguinte correlação:
Logo
Sendo que esse é tabelado. Aqui vou dar uns exemplos pra gente:
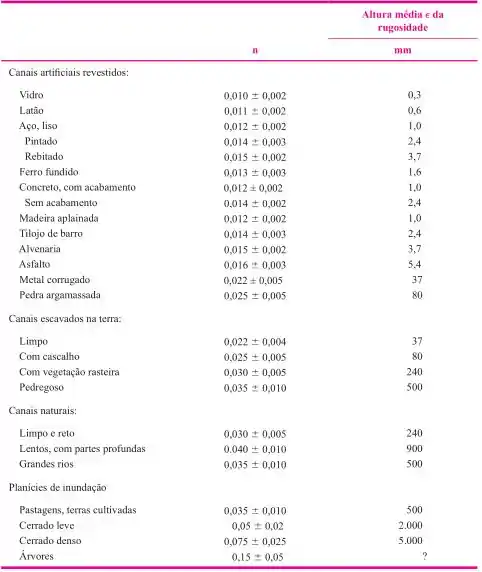
Veja que as duas fórmulas são válidas, então fica a gosto do freguês.
Muita informação eu sei, mas vamos dar uma praticada que tudo ficará mais claro.
Fórmula de Chézy
Exercícios Resolvidos
Exercício Resolvido #1
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Um canal retangular tem 2 m de largura e contém água com 3 m de profundidade. Se a declividade for de 0,85° e o revestimento for de metal corrugado, calcule o valor da descarga para escoamento uniforme.
Passo 1
Vamos esquematizar a seção dessa canal para entendermos melhor o que está acontecendo:
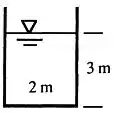
Neste exercício, precisamos calcular a “desacarga” ou simplesmente a vazão do canal.
Vimos nessa teoria que a velocidade é
Vamos então calcular o raio hidráulico a declividade e a componente de atrito do metal corrugado e então lembrar daquela fórmula clássica:
Passo 2
Vamos começar pelo mais chatinho que é calcular o raio hidráulico:
Que é a área da seção sobre o perímetro molhado:
Logo :
Passo 3
O atrito que vamos utilizar na fórmula da velocidade é o do metal corrugado, olhando aquela tabelinha que forneci na teoria, o número de Manning é de:
E sabemos também que
Aplicando na fórmula da velocidade:
Multiplicando pela área temos a vazão
Resposta
A descarga é de .
Exercício Resolvido #2
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
O canal trapezoidal da figura é feito de alvenaria e tem declividade de 1:500. Determine a vazão se a profundidade normal for de 80 cm.

Passo 1
Este exercício é bem parecido com o anterior, a grande diferença é a forma como a declividade foi escrita e claro a seção ser trapezoidal.
Vamos primeiro calcular a área da seção e o perímetro molhado, depois analisamos a questão da declividade.
Passo 2
Sabemos que a expressão do raio hidráulico é
Calculando :
Podemos dividir a figura em três áreas: dois triângulos retângulos e um retângulo.
A área do retângulo é simplesmente:
Já a dos triângulos devemos encontrar o valor da “base”
Por trigonometria:
Logo a área de cada triângulo é:
Logo a área total é
Para o perímetro molhado devemos calcular o valor da hipotenusa de cada triângulo:
Logo, por trigonometria:
Portanto o perímetro é
O raio hidráulico calculado então:
Passo 3
Neste caso a declividade já está calculada e é exatamente , logo substituindo na fórmula da velocidade, para
Passo 4
Pela fórmula da vazão:
Resposta
Exercício Resolvido #3
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Cinco tubos de esgoto, cada um com 2 m de diâmetro e feitos de argila, funcionam a meia seção, com uma declividade de 0,25°, descarregando em um único tubo feito de asfalto, também com declividade de 0,25°. Se o tubo maior também deve funcionar a meia seção, qual deverá ser seu diâmetro?
Passo 1
Neste probleminha, as coisas continuam parecidas com os outros exercícios.
Calcularemos o raio hidráulico, velocidade... Mas como a vazão deve ser constante, poderemos calcular o diâmetro necessário do tubo maior.
Vamos com calma e uma hora a gente chega lá.
Vamos começar com o raio hidráulico
Passo 2
Para isso devemos montar a expressão do raio:
Como o tubo está “meio-cheio” ou “meio-vazio” dependendo de quão otimista você é:
Logo
Passo 3
A vazão de cada tubo é dada por:
Onde
Como são cinco tubos de esgoto:
Substituindo o que conhecemos:
Sendo e , supondo que o fundo seja de tijolos de argila, o exercício não deixou claro:
Logo
Passo 4
Agora faremos o mesmo processo só que meio que ao contrário, saíremos da vazão para o raio, vamos montar uma expressão pra isso, chega mais!
Sabemos que
E que
E
Substituindo na expressão da vazão:
Vimos que para um tubo circular “meio-cheio”:
Logo
Rearrumando os termos:
Passo 5
Como queremos , devemos colocar de um lado e todos termos do outro:
Elevando ambos os lados a :
Substituindo tudo que conhecemos:
Resposta
Exercício Resolvido #4
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Um canal retangular feito de tijolos com é projetado para conduzir de água em escoamento uniforme. Discute-se se a largura do canal deverá ser de 1,22 ou 2,44 m. Qual o projeto requer menos tijolos? Em que percentual?
Passo 1
Fala jovem!
Então esse probleminha é só mudando um pouco a ordem das coisas que a gente tava vendo, ao invés de calcular a vazão calcularemos em outras palavras o raio hidráulico de cada situação.
Não é bem o raio mais uma das componentes que ele depende que é o perímetro molhado do canal.
Vamos então começar escrevendo esse raio hidráulico em função da largura e da profundidade:
Sendo a profundidade e a largura.
Passo 2
A fórmula da vazão é
Se elevarmos a expressão em , e rearrumarmos, terminamos com a seguinte expressão:
Passo 3
Temos um problema, não existe um método analítico para resolver esse exercício, mas se você tem uma calculadoraé possível convergir para um valor. O que faremos é tentar colocar um valor de que zere a expresão abaixo:
Para isso basta montar a expressão e ir por tentativa e erro mudando , até chegar em um valor próximo a zero.
Calcularemos a profundidade em ambos casos de e :
:
:
O projeto que menos requer tijolos é o de menor perímetro molhado. Logo é o segundo.
Que requer:
da quantidade de tijolos do outor projeto.
Resposta
O segundo projeto requer menos tijolos, e requer do outro projeto ou a menos.
Exercício Resolvido #5
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Em períodos de cheia, um canal natural frequentemente consiste em uma calha principal profunda mais duas calhas de cheia, como mostra a figura. As calhas de cheia em geral são rasas e rugosas. Se o canal tem a mesma declividade em todos os pontos, como você analisaria essa situação em relação à vazão? Admita que , , , , e , com uma declividade de 0,0002. Calcule a vazão em m3/s.
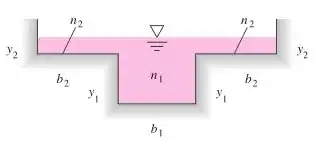
Passo 1
Nossa abordagem neste problema é dividí-lo em dois “canais” diferentes, já que temos dois valores de e não existe uma expressão que combina ambos em uma expressão só, como se criássemos um atrito equivalente.
Portanto calcularemos a vazão no canal fundo e nos canais rasos de cheia.
Passo 2
Para o canal fundo temos que o raio hidráulico:
A vazão é determinada por
Passo 3
O mesmo procedimento, mas agora para os canais rasos:
A vazão de cada canal:
Passo 4
Somando todas vazões:
Resposta
Exercício Resolvido #6
Concurso Analista Judiciário – Especialidade: Engenharia – CESPE - 2015
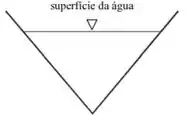
A partir da figura acima, que ilustra a seção transversal de um canal triangular aberto, assinale a opção correta acerca de hidráulica aplicada em canais abertos.
(A) O perímetro molhado corresponde ao resultado da soma dos comprimentos das faces em contato com a água com o comprimento da superfície da água
(B) O raio hidráulico corresponde ao comprimento de uma das faces do canal em contato com a água
(C) A profundidade de escoamento equivale à distância vertical entre o vértice no fundo do canal e a superfície da água.
(D) A borda livre deve ser considerada no cálculo do perímetro molhado.
(E) A velocidade máxima da água em canais desse tipo ocorre no vértice inferior do canal triangular
Passo 1
E aí, jovem mestre! Vamos relembrar o que aprendemos na teoria. O perímetro molhado é a soma dos lados do canal que são molhados pelo fluido.
É justamennto por isso que sua definição não inclui a superfície da água ou borda livre. Logo, as afirmações A e D estão erradas.
Vimos na teoria que o radio hidráulico é esse carinha aqui:
Ou seja, o raio hidráulico é a área dividida pelo perímetro molhado, ou simplesmente, um quarto do diâmetro hidráulico. Analisando essa definição, não podemos dizer que o raio hidráulico corresponde ao comprimento de uma das faces do canal em contato com a água...
Logo, a afirmação B também está errada.
A letra C diz que a profundidade de escoamento é a distância vertical entre o vértice no fundo do canal e a superfície da água. Como esse vértice é o ponto mais profundo do canal, essa afirmação é verdadeira e a resposta é a letra C :D
Antes de terminar, vamos ver por que a E não está certa. No vértice inferior do canal triangular mostrado, a velocidade do fluido é a velocidade do canal pela condição de não-deslizamento.
Geralmente essa velocidade no fundo é zero, pois o canal costuma estar parado. Logo, a velocidade máxima não fica no fundo e a letra E está errada.
A afirmação C é a única verdadeira dentre essas 5.
Resposta
C
Exercício Resolvido #7
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 776, ex. 11.42
Um canal retangular com 2 m de largura e inclinação de 0,0005 possui uma profundidade de escoamento de 1,5 m. O coeficiente de rugosidade de Manning é de 0,015. Determine a descarga uniforme em regime permanente no canal.
Passo 1
Vamos começar ilustrando o escoamento e identificando as variáveis dadas no enunciado? Partiu!
O canal é retangular, então essa é uma visão de um corte nele:
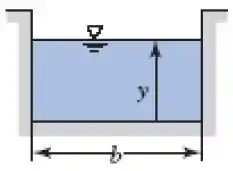
Do enunciado sabemos que
O exercício pede a descarga uniforme desse escoamento permanente. Ou seja, queremos saber a vazão! Na teoria, vimos uma fórmula que Manning ajudou a simplificar para achar a velocidade. 😉
A partir da velocidade, conseguimos encontrar a vazão volumétrica, já que: . Então vamos substituir o V
Lembrando que a área é a área da seção transversal (justamente a área do corte)
Além disso, o raio hidráulico é
Afinal, quem é o perímetro molhado ? É o somatório dos comprimentos em que o fluido toca no canal. O perímetro molhado é a parte laranja (destacada) da figura:
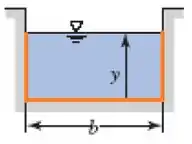
Atualizando o raio hidráulico
Show! Substituindo essa galera toda aí na expressão da vazão
Passo 2
Agora que conhecemos todas as variáveis, vamos substituir
Fazendo as contas na calculadora
Essa é a descarga uniforme em regime permanente 😉
Resposta
Exercício Resolvido #8
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 776, ex. 11.43
Determine a profundidade de escoamento uniforme em um canal retangular com 2,5 m de largura com uma descarga de 3 m³/s. A inclinação é 0,0004 e o fator de rugosidade de Manning é 0,015.
Passo 1
Esse é um exercício de canal retangular é um pouquinho diferente do que vimos até agora, por que ao invés de querer saber a vazão, queremos saber a profundidade y.
Desenhando conseguimos entender melhor, então bora lá! Canal retangular
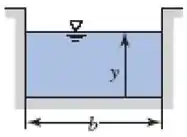
Beleza! Agora vamos organizar os dados do enunciado para saber quem já conhecemos e quem precisamos calcular
Largura:
Descarga ou vazão:
Inclinação ou declividade:
Coeficiente de rugosidade de Manning:
Ótimo! O enunciado já deu bastante informação. Aliás, ao dizer o coeficiente de Manning, sabemos que podemos usar essa fórmula que vimos na teoria
Só que o exercício não deu a velocidade, mas informou a vazão, que é . Então vamos transformar essa fórmula
Como (área transversal do canal) e o raio hidráulico é
Sendo que o perímetro molhado é , pois é a parte do canal que o fluido molha (conforme está destacado na figura)
Então a vazão fica assim:
Passo 2
Assim, nós conseguimos ter uma equação com variáveis conhecidas e apenas o y é desconhecido. Então vamos substituir juntos e ver no que dá
Isolando as constantes
Eeeeita! E como a segura a barra que é resolver uma equação em que y está implícito? Esse termo aqui não está ajudando a gente a isolar o y...
Pera lá que o forninho não vai cair não! Temos algumas opções para resolver isso, podemos aplicar Newton Raphson, ou usar o Excel, ou aquela calculadora que resolve esse tipo de equação.
Ou a gente pode chutar um valor inicial para y, fazer essa conta aqui e comparar o qual próximo isso está de 0,9. Dependendo do resultado, vamos melhorando nosso chute, até chegar num valor bem próximo, que será a resposta :D
Para y = 1
Bem, 0,676 está distante de 0,9. Então vamos aumentar y.
Para y = 1,5
Agora, o resultado está menos distante de 0,9, porém, está maior que o desejado. Próximo y deve estar entre 1 e 1,5
Para y = 1,3
Estamos próximos de 0,9, mas um pouco acima!
Para y = 1,2
Opa! Sabemos que y está entre 1,2 e 1,3. Já é um intervalo pequeno
Para y = 1,25
Para ser um pouco mais preciso
Para y = 1,24
0,904 está bem próximo de 0,9! Então nós encontramos y, que é 1,24 m. :D
Repara que esse exercício foi um pouco mais trabalhoso porque foi pedida a profundidade y e ela estava implícita na equação. Partiu fazer mais exercícios? Continua aí :D