Pressão Hidrostática
Produzido por Raphael EloiTeoria
A pressão hidrostática é a pressão que uma coluna de fluido em repouso exerce sobre um corpo.
Hoje você vai aprender tudo o que você precisa pra conseguir resolver todos os exercícios de pressão hidrostática! 🤩 😉
Então pra começar com tudo, se liga nesse vídeo super completo sobre pressão hidrostática 👇
📢 Clique para saber mais:
Fórmula da Pressão Hidrostática - Teorema de Stevin
O Teorema de Stevin diz o seguinte:
“A diferença entre as pressões de dois pontos de um fluido em equilíbrio (repouso) é igual ao produto entre a densidade do fluido, a aceleração da gravidade e a diferença entre as profundidades dos pontos”
Escrevendo isso em fórmula, temos que:
Onde,
Vamos sempre ter em mente que a pressão varia apenas com a profundidade vertical do fluido e nunca com a posição horizontal!
Ué, mas até nesses casos?! 👇👇👇

SIM! Até nesses casos! Chamamos esse fenômeno de Paradoxo hidrostático!
Pressão sob vários Fluidos
Vimos como calcular a pressão, porém falamos apenas de um único fluido. Agora, como você calcularia a pressão no fundo do recipiente nesse caso aqui:
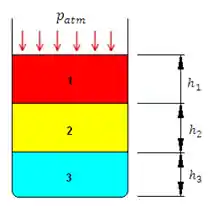
Não tem mistério! Tudo o que precisamos fazer é somar separadamente a pressão exercida sobre cada fluido com densidade diferente:
E claro, se queremos saber a pressão total no fundo do recipiente, precisamos somar a pressão atmosférica!
Princípio de Pascal - Vasos Comunicantes
O princípio de Pascal diz que: “O acréscimo de pressão produzido num líquido em equilíbrio transmite-se integralmente a todos os pontos do líquido”.
Podemos escrever a seguinte relação para vasos comunicantes:
Esse conceito é muito útil em elevadores ou prensas hidráulicas. Bora entender como ele funciona na prática?
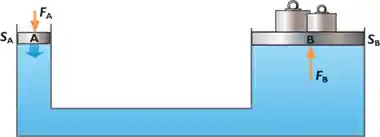
A pressão exercida pela força
Vamos equacionar isso que acabamos de falar. Qual é a pressão feita pela força
A pressão será transmitida igualmente, assim:
A força gerada será de acordo com a área do lado B:
Substituindo o valor da pressão
Com essa equação podemos ver que fazendo uma pequena força, podemos aumentar ela de acordo com a razão
Reorganizando a equação, temos:
Exatamente a relação que vimos lá em cima!
Agora, vamos praticar com exercícios?!
Fórmula da Pressão Hidrostática - Teorema de Stevin
Princípio de Pascal - Vasos Comunicantes
Exercícios Resolvidos
Exercício Resolvido #1
Qualquer valor de pressão medida pode ser expresso como um comprimento ou carga, . Qual é a pressão padrão ao nível do mar expressa em (a) de glicerina, (b) de Hg, (c) de coluna de água e (d) de etanol? Considere que todos os fluidos estejam a 20°C.
Dados: 
Passo 1
Primeiro vamos entender de onde ele tirou isso que a pressão pode ser expressa como comprimento ou carga.
No futuro vamos chamar a pressão hidrostática de carga. Bem, dado que a densidade e a gravidade são “constantes” podemos representar a pressão simplesmente pela altura de um fluido. Por isso o que o enunciado fez foi pegar a equação da pressão que vimos:
E isolar a altura, assim:
Desta forma dada uma pressão e o fluido descobrimos o comprimento de fluido necessário para atingir aquela pressão.
Certo, que pressão que o enunciado quer saber? É a pressão do nível do mar.
A pressão do nível do mar é a pressão que usamos como padrão para representar a pressão causada pela atmosfera. Por isso conhecida como pressão atmosférica.
O valor da pressão atmosférica é:
Lembrando que a unidade Pascal tem mesmo valor que o .
Esse último valor é o que usamos para comparar. Pra gente a comparação é muito importante, assim definimos a pressão atmosférica como padrão, valendo e comparamos com as outras pressões, por exemplo falar que 10 metros de água vale , que vale .
Mas então, nessa questão queremos saber qual o comprimento de fluido que representa a pressão no nível do mar .
Passo 2
Queremos saber o comprimento de glicerina que representa a pressão atmosférica. Para isso precisamos saber o valor da pressão atmosférica em já sabemos , precisamos saber da densidade da glicerina a , é dado pela tabela, e pro fim da aceleração da gravidade que a gente sabe de tanto que usamos ela:
Assim, podemos aplicar a fórmula dada pelo enunciado:
Passo 3
agora quanto essa pressão equivale em milímetros de mercúrio?
Basta substituir a densidade dos fluidos na formula:
O que equivale a 763 mm de mercúrio.
Passo 4
Fazendo o mesmo para a água temos:
Passo 5
Fazendo o mesmo para o etanol temos:
Isso em milímetros equivale a .
Resposta
Exercício Resolvido #2
Considerando e , o valor da pressão manométrica atuante nos ouvidos de um mergulhador na água , correspondente a três vezes a pressão atmosférica, está associado a uma profundidade, em , de:
Passo 1
Na questão anterior falamos de que usamos muito de comparação, essa questão é um exemplo.
A questão diz que metros de água corresponde a 3 vezes o valor da pressão atmosférica . Nosso dever é descobrir quanto vale .
Para isso vamos usar a nossa equação da pressão
Sem o pois o enunciado refere à pressão manométrica.
Como queremos a altura de água, vamos isolar :
a pressão nós temos , a densidade da água foi dada e o valor da gravidade o enunciado pediu para usarmos .
Substituindo os valores temos:
Resposta
Alternativa
Exercício Resolvido #3
Devido a diferenças de temperatura, ou a presença de sal ou, ainda, de sedimento, um fluido homogêneo em condição estática pode estratificar. Neste contexto, calcule a pressão relativa em um ponto de um líquido distante H da superfície livre, se a massa específica do fluido for variável e dada por: , em que é a massa específica na superfície e é uma constante.
Passo 1
Fizemos alguns exercícios onde apenas aplicamos a equação
Mas na teoria vimos que essa equação só é valida quando densidade e gravidade são constantes. Bem, nesse caso a densidade ou massa específica não são constantes quando variamos a altura assim, temos que voltar lá na integral da teoria:
O enunciado nos deu a equação com que a densidade varia :
Assim, temos que:
A gravidade ainda é constante então temos:
Como a integral de uma soma é igual a soma das integrais temos:
Beleza são duas integrais polinomiais, assim a solução delas são:
A equação da pressão no final é:
Resposta
Exercício Resolvido #4
O ponto mais profundo conhecido nos oceanos é 11.034 metros no Mariana Trench no Pacífico. Nessa profundidade o peso específico da água do mar é aproximadamente de . Na superfície, . Calcule a pressão absoluta nessa profundidade, em atm.
Passo 1
Novamente não podemos simplesmente aplicar , pois a densidade do fluido varia conforme a altura.
Mas o enunciado forneceu o peso específico, que é a densidade vezes a gravidade, e denominamos como . Assim temos que: é substituído por .
O pior é que não temos a equação de como varia esse peso especifico. Como a variação é de menos de em , vamos aproximar a variação por uma variação linear da forma que
Assim temos duas incógnitas e
Assim, vamos usar o segundo valor de peso específico fornecido pelo enunciado que é o peso específico da água na superfície, ou seja, .
Assim:
Agora com a primeira densidade vamos descobrir o valor de .
Isolando , temos:
Beleza, assim a equação que descreve o peso específico da água é:
Passo 2
Agora que sabemos como o peso específico varia, podemos voltar na integral da pressão e integrar corretamente
Integrando de forma igual feita no exercício anterior, temos:
Como fizemos uma integral indefinida, pois a questão quer pressão absoluta, então devemos levar em conta a pressão atmosférica, temos:
Como enunciado quer a resposta em , temos que lembrar que
Assim,
Isso quer dizer que nessa profundidade a pressão exercida é mais de mil vezes maior que a pressão da atmosfera.
Resposta
Exercício Resolvido #5
O sistema na Figura abaixo está a . Se a pressão atmosférica é de e a pressão no fundo do tanque é de , qual é a densidade do fluido X?
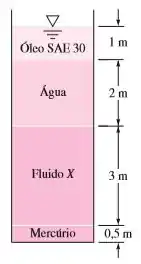
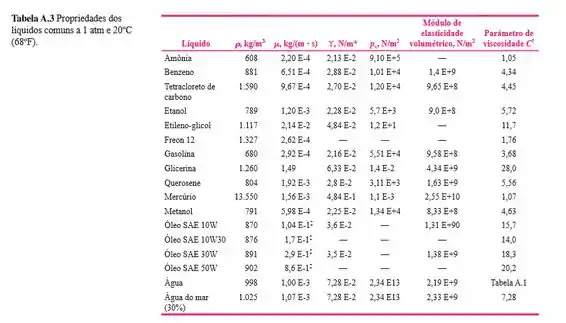
Passo 1
Até agora só havíamos visto questões com um único fluido, pois bem agora temos vários. Mas não é motivo para se preocupar. Vimos na teoria que quando temos mais de um fluido a pressão é dada por:
Nesse caso temos liquidos. Temos a pressão no fundo do recipiente, a pressão atmosférica, pela tabela conseguimos descobrir a densidade de 3 dos fluidos e pela imagem temos a altura da coluna de cada fluido.
Assim, temos todas as informações da equação acima, exceto a densidade do fluido , possibilitando que descubramos quanto vale essa densidade.
Então vamos lá: ; ;
Ainda temos: ; ; ; e
Substituindo na equação temos:
Isolando , temos:
Ao calcularmos isso, temos:
Opa! Então encontramos a massa específica do fluido X:
Agora pra gente encontrar a densidade é só dividir a nossa massa específica pela massa específica da água, então temos:
Substituindo os valores, ficamos com:
A densidade do fluido X será:
Resposta
Exercício Resolvido #6
O medidor de combustível do tanque de gasolina de um carro fornece uma indicação proporcional à pressão manométrica do fundo do tanque, como na Figura abaixo. Se o tanque tiver de profundidade e acidentalmente contiver de água mais gasolina, quantos centímetros de ar permanecerão na parte superior quando o medidor indica erroneamente “tanque cheio”?
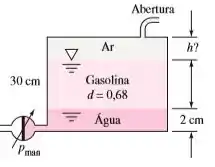
Passo 1
Primeiro devemos saber quando o tanque vai acusar que o tanque está cheio. Como o enunciado disse isso acontece por um medido de pressão.
Então o certo seria, quando o tanque tivesse cheio de gasolina, somente gasolina, ele apontaria que o tanque está cheio. Como? Bem alguém ajustou um indicador que quando o medidor de pressão apontasse a pressão exata que de gasolina exerce ele ia indicar que o tanque está cheio.
Que pressão é essa, a gente vai calcular usando . Sem a pressão atmosférica pois o medidor é um manômetro, que vimos na teoria que ele calcula a pressão exercida apenas pelo fluido, tirando a atmosférica.
Beleza, então a pressão que indica tanque cheio é:
Quando a densidade é dada sem unidade, significa que estamos considerando a da água igual a e a altura deve ser usada em m. E a pressão calculada será em .
Assim,
Passo 2
Agora, vamos ter que descobrir qual a altura de gasolina, mais de águas corresponde a pressão de .
A fórmula de pressão para mais de um fluido é
A densidade a gente sabe dos dois fluidos, a altura de água também, a pressão resultante também, então temos tudo para descobrir a altura de gasolina.
Agora vamos ver quanto do tanque será ocupado pelo ar. A altura do tanque é sendo que está ocupado por água e com gasolina, assim a altura da coluna de ar será de 0,93.
Resposta
Exercício Resolvido #7
O tanque cilíndrico na Figura abaixo está sendo cheio com água a por uma bomba que desenvolve uma pressão de saída de . No instante mostrado, a pressão no ar é de e . A bomba para quando ela não pode mais aumentar a pressão da água. Para compressão isotérmica do ar, calcule H naquele instante.
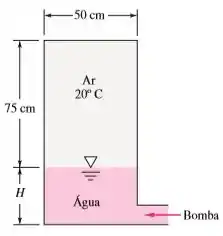
Passo 1
A bomba vai parar de encher o tanque de água quando a pressão no tanque for igual a pressão que ela exerce. Assim:
Nesse momento teríamos uma coluna de água . E de ar igual a , pois a altura do tanque é de .
Então teríamos a seguinte equação:
Para resolvermos o problema precisamos encontrar o valor da pressão final de ar. O que é fácil se lembrarmos de termodinâmica. Da fórmula “PiViTi-PoVoTo”. Como é uma compressão isotérmica, temos:
Então para encontrarmos o valor de , precisamos encontrar a forma com que a pressão de ar irá variar de acordo com o valor de .
Passo 2
Então se tivermos a pressão no início, o volume no início, e o volume no final, descobrimos a pressão no final por uma regra de três.
A pressão no início é dada pelo enunciado
Agora vamos calcular o volume inicial. O volume de um cilindro é área da base vezes altura.
Chamando a área da base de , temos que o volume ocupado por no início era de:
E o volume final será em função de , sendo assim:
Passo 3
Agora temos tudo para descobrir a pressão final
Agora sim, temos tudo em função de .
Passo 4
Tendo tudo em função de , podemos substituir na equação de pressão no final:
Agora teremos uma equação do segundo grau assim:
Resolvendo a equação do segundo grau, achamos dois valores
e
Como o tem que ser menor que o único valor possível é
Resposta
Exercício Resolvido #8
Na Figura abaixo, a força hidrostática é a mesma no fundo dos três recipientes, apesar de os pesos dos líquidos acima serem muito diferentes. As três formas dos fundos e os fluidos são iguais. Isso é chamado de paradoxo da hidrostática. Explique por que ele é verdadeiro e desenhe um corpo livre de cada uma das colunas de líquido.
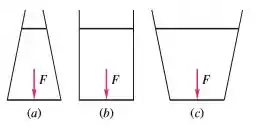
Passo 1
Vimos na teoria que a pressão no fundo de um recipiente é função apenas da densidade e altura do liquido.
Como nos três recipientes o liquido é o mesmo e a altura é a mesma e estão todos exposto a mesma atmosfera então temos que a pressão no fundo dos três recipientes são iguais.
Como a pressão é definida como:
Onde é força e área do fundo do recipiente. Temos que a força no fundo do recipiente será:
A pressão a gente sabe que é igual nos três recipientes e o enunciado falou que a área do fundo neles também são iguais, sendo assim a força no fundo é a mesma.
Passo 2
Desenhar o corpo livre de cada uma das colunas é esquematizar as forças atuantes nos recipientes.
As forças que vamos representar é força causada pela pressão atmosférica. A força peso, e a força de reação nas paredes do recipiente devido ao contato com o fluido.
Poderíamos representar a força de reação no fundo do recipiente, mas essa como o enunciado já mostrou que a força atuante lá é igual a força resultante também seria.
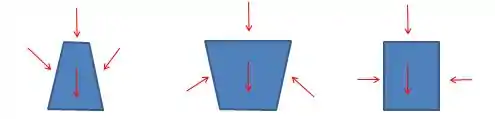
O legal de observar é que como o peso na do meio é maior que em todas, as paredes do recipiente fazem força para cima, compensando esse peso extra, fazendo com que assim a força no fundo seja igual. O inverso acontece no primeiro. Como o peso de liquido é menor a parede do recipiente reage para baixo assim, aumentando a força fazendo que no fim todas fiquem iguais.
Paradoxo é algo difícil de se aceitar, por isso que você ainda não acredita muito nisso é normal. Não se preocupe muito com isso, apenas lembre que a pressão depende apenas da altura e do liquido. Isso que importa.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #9
Na Figura abaixo, a comporta de cobertura AB fecha uma abertura circular de de diâmetro. A comporta é mantida fechada por uma massa de como mostra a figura. Suponha a gravidade padrão a . Em que nível da água a comporta será deslocada? Despreze o peso da comporta
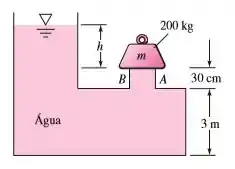
Passo 1
Para a comporta se deslocar a pressão exercida pela água deve ser maior que a pressão exercida pelo peso.
Então primeiro vamos descobrir qual é a pressão exercida pelo peso.
A força é . Como temos um círculo, a área é dada por e ela também pode ser escrita em função do diâmetro( ). E aí obtemos que , assim a pressão será:
Agora, lembra do princípio de pascal que diz que qualquer adição de pressão será transmitida integralmente pelo fluido.
Então, a pressão devido a coluna de líquido acima da altura da comporta é uma pressão adicional, que quando essa pressão for maior que a pressão causada pelo peso a comporta ira se mover.
Sendo assim a pressão no lado esquerdo deve ser igual a pressão causada pela comporta.
Assim:
Resposta
Exercício Resolvido #10
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
O macaco hidráulico da Figura abaixo está cheio com óleo a . Desprezando o peso dos dois pistões, qual a força que é necessária na alavanca para suportar o peso de indicado no desenho?
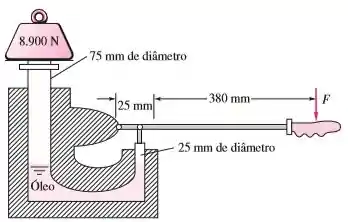
Passo 1
Essa é uma questão de transmissão de força, de multiplicar a força usando um sistema hidráulico.
Isso nos remete a Pascal e como vimos na teoria:
A força no lado é e a área desse pistão é
E a área do lado é de
Assim, conseguimos descobrir a força necessária que seja aplicada no pistão para suportar o peso em .
Passo 2
Agora que descobrimos o valor da força que deve ser aplicada no pistão , conseguimos através de equilíbrio de momento descobri qual o valor da força na alavanca irá gerar essa força .
Fazendo equilíbrio de momento temos:
O ponto analisado será o inicio da alavanca. Senso assim a força está a desse ponto e a força está .
A equação de momento será:
O referencia de sinal adotado foi girar no sentido horário negativo, por isso e girar no sentido anti-horário positivo.
Agora podemos descobrir o valor de .