Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 20

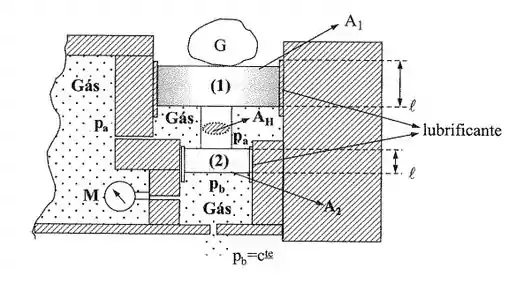
O pistão da figura desce com velocidade constante de 5   m / s . Dados: espessura da camada lubrificante 0,001   m ; v = 10 - 3   m 2 / s ; γ = 8.000   N / m 3 ; P a =   10   k P a ; G = 100   N ; D 1 = 16   c m ; D 2 = 8   c m ; A H = 20   c m 2 ;   l = 5   c m ; P a t m = 100   k P a ; g = 10   m / s 2 ;   despreza-se o peso do pistão. Pede-se:

  1. a força resistente oferecida pelo lubrificante ( F μ ) ;
  2. a pressão absoluta p b ( c t e ) ;
  3. a leitura do manômetro M .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O item “a” nos pede a força resistente oferecida pelo lubrificante. Essa força é calculada a partir da equação da Lei de Newton da viscosidade:

F μ = τ ⋅ A l

Onde:

τ = μ v ε

Como o lubrificante está agindo em duas áreas, podemos dizer que:

F μ = F μ 1 + F μ 2

Estas forças irão se diferenciar apenas na área de aplicação, portanto:

F μ 1 = μ v ε ⋅ π D 1 l

E:

F μ 2 = μ v ε ⋅ π D 2 l

Logo:

F μ = μ v ε ⋅ π D 1 l + μ v ε ⋅ π D 2 l

F μ = μ v ε ⋅ π D 1 + D 2 l

Passo 2

O coeficiente de atrito dinâmico pode ser dado por:

μ = v γ g

Logo:

F μ = v γ g ⋅ v ε ⋅ π D 1 + D 2 l

Agora é só substituir os valores e calcular a força:

F μ = 10 - 3 8000 10 ⋅ 5 0,001 ⋅ π 0,16 + 0,08 0,05

Resolvendo, temos que:

F μ = 150,79   N

Passo 3

O item “b” nos pede a pressão p B . Se descobrirmos a força F 2 e dividirmos pela área A 2 , encontraremos p B .

Analisando as forças, temos o seguinte arranjo:

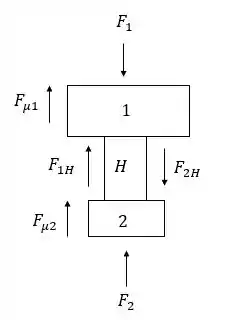
Analisando a condição de equilíbrio, temos que:

F 1 + F 2 H = F 2 + F 1 H + F μ 1 + F μ 2

Temos que:

F 1 H = p a A 1 - A H

F 1 H = 10 ⋅ 10 3 π ⋅ 0,16 2 4 - 20 ⋅ 10 - 4

F 1 H = 181,06   N

E:

F 2 H = p a A 2 - A H

F 2 H = 10 ⋅ 10 3 π ⋅ 0 , 08 2 4 - 20 ⋅ 10 - 4

F 2 H = 30,27   N

Passo 4

Portanto, substituindo pelos valores, temos que:

100   N + 30,27   N = p b π ⋅ 0,08 ⋅ 0,05 + 181,06   N + 150,79   N

Resolvendo, encontramos:

p b = - 39908   P a

Como queremos a pressão absoluta, temos que:

p b , a b s = p b + p a t m

Logo:

p b , a b s = - 39908 + 100000

p b , a b s = 60092   P a

Passo 5

A pressão no manômetro, solicitada no item “c” é dada pela diferença entre a pressão interna p b e a pressão externa p a :

p m = p b - p a

p m = - 39908 - 10000

p m = - 49908   P a

Resposta

a )   F μ = 150,79   N

b )   p b , a b s = 60092   P a  

c ) p m = - 49908   P a  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O ponto mais profundo conhecido nos oceanos é 11034 metros no Mariana Trench no Pacífico. Nessa profundidade o peso específico da água do mar é aproximadamente de 10520 N / m 3 . Na superfície, γ ≈ 10
A cidade de Denver, no Colorado, tem uma altitude média de 1590 m. Em um dia normal (Tabela A.6), o medidor de pressão manométrica A em um experimento de laboratório indica 83 kPa e o medidor B indica
Para gases submetidos a grandes mudanças de altitude, a aproximação linear, Equação (2.14), é imprecisa. Expanda a lei de potência da troposfera, Equação (2.20), em uma série de potências e mostre que
Um tubo piezométrico de vidro limpo vertical tem um diâmetro interno de 1 mm. Quando é aplicada a pressão, água a 20°C sobe no tubo até a altura de 25 cm. Após corrigir para a tensão superficial, calc
Uma mina de diamantes está a 3200 m abaixo do nível do mar. (a) Calcule a pressão do ar nessa profundidade. (b) Se um barômetro, com precisão de 1 mm de mercúrio, for levado para dentro dessa mina, co