Vazão e Volume de Controle
Produzido por Raphael EloiTeoria
Vazão Volumétrica
Lá na Estática dos Fluidos nós estudamos o fluido paradinho (estátua!). Só que agora, vamos estudar a Cinemática dos Fluidos. Sabe o que isso quer dizer? :D Quer dizer que vamos estudar o fluido em movimento. Yes!
Já que o nosso fluido está fluindo, escoando, se movimentando agora, uma variável que vai nos acompanhar daqui para frente é a famosa Vazão! A vazão nos diz a quantidade de fluido que está escoando num determinado período. Certo?
Agora, tenho outra notícia importante para te dar. Vamos nos deparar com dois tipos de vazões diferentes: a volumétrica e a mássica. Como o nome já diz, a vazão volumétrica diz o quanto de volume está passando naquele período e a vazão mássica diz o quanto de massa está passando naquele período.
No Sistema Internacional, a unidade de vazão volumétrica (Q) é e a unidade de vazão mássica ( é . Fechado?
E quanto aos números? Como eu encontro a vazão volumétrica? Quando estudamos vazão vimos que ela é função da velocidade () e da área ():
Assim, a vazão volumétrica de um objeto é:
É através dessa equação que iremos encontrar a vazão de uma superfície em um escoamento.
E a vazão mássica, como que fica?
A vazão mássica é dada pelos mesmos termos que a vazão volumétrica, mas também precisa da massa específica () :
Bem, pela conservação da massa e sabendo que não vamos acumular nada no nosso sistema, sabemos que toda a vazão que entrar vai ter que sair, né? “Nada se cria, nada se perde, tudo se transforma”. Concordamos com Lavoisier, não é mesmo?

Então,
Mas qual é a relação entre Vazão Volumétrica e Vazão Mássica?
Aí mora o x da questão! Aqui em MecFlu, nessa parte da matéria, costumamos trabalhar com fluidos incompressíveis (que não conseguem se comprimir). Ou seja, a massa específica desses fluidos ρ desses fluidos é constante.
Então, podemos escrever a conservação da massa assim:
Como ρ é constante para os fluidos incompressíveis, podemos usar para eles
Assim, conseguiremos resolver o início de vários problemas montando a equação de vazão. Show de bola! 😉
Volume de Controle
Outra coisa muito importante para estudar Cinemática dos Fluidos é o Volume de Controle. Carinhosamente, vamos chamá-lo de VC.
Agora, queremos analisar o resultado do escoamento sobre um espaço, como a interação casco do navio com a água. Como faremos isso, vamos ter que analisar a interação de partícula com partícula?
Não! E é por isso que esse capítulo se chama Forma Integral para Volume de Controle. Justamente porque vamos olhar nossos sistema de forma macro (tudo o que está entrando e tudo o que está saindo) e não micro (interações partícula-partícula).
Para nos ajudar foi desenvolvido um “jeitinho” que permite com que obtenhamos esses resultados que não resultados do sistema, o jeitinho criado foi a utilização de um volume de controle.
O que é o volume de controle? É uma região escolhida por nós que engloba o escoamento do fluido que iremos analisar. Para isso é necessário escolher uma região que o fluido escoe por ela.
Imagine água escoando por uma tubulação e você deseja saber a variação de energia que o fluido tem quando sai da região para a :
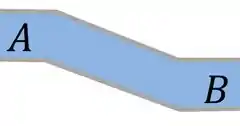
Escolha do Volume de Controle
Qual dos três volumes de controle você acha que seria capaz de nos dar a resposta que queremos: Laranja? Vermelho? Ou Roxo?
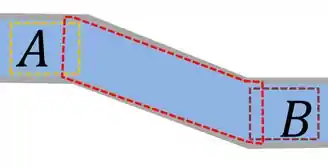
Se fossemos usar o laranja seriamos capazes de obter apenas as propriedades da região , se usássemos o roxo seríamos apenas capazes de estudar a região . Já o volume de controle de controle vermelho esse engloba o liquido na região e , possibilitando assim que analisemos a diferença entre a energia nessas regiões.
A dica é escolher o volume de controle que englobe as variáveis que você precisa descobrir para resolver o exercício e as variáveis que o enunciado já te deu!
Vamos as propriedades do volume de controle
Como o nome já diz é um volume. Mas eu acabei de representar com uma superfície?!!!
Não, não, aquilo é um volume, onde você só está vendo uma superfície. Como não conseguimos representar as dimensões a profundidade que normalmente é constante não é representada. Mas nunca esqueça que isso é um volume e existe uma profundidade. Isso é importante para os próximos itens.
O volume de controle sempre terá duas superfícies nas quais o fluido irá escoar atravessando-a (perpendicularmente se possível). Uma será a superfície de entrada e a outra será a superfície de saída. É aqui que entra a profundidade.
Imagina aí que no exemplo anterior o cano tem 1 metro de altura e profundidade de , assim a superfície do volume de controle de entrada seria a superfície formada pela altura e profundidade do cano, mais especificamente, seria a secção reta do cano.
O volume de controle é um conceito, ele não está lá de verdade, sendo assim não pode alterar nada no escoamento.
Ele ainda pode ser fixo, móvel e até deformável.
Deu pra entender tudo até agora? Pareceu difícil?

Com o tempo isso vai se tornar simples, vamos treinar a escolha e equações que esse volume de controle irá gerar.
Partiu praticar a escolha do volume de controle e o cálculo das vazões? Exercita aí! 😊
E a vazão mássica, como que fica?
Mas qual é a relação entre Vazão Volumétrica e Vazão Mássica?
Volume de Controle
Escolha do Volume de Controle
Vamos as propriedades do volume de controle
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
A vazão volumétrica de um fluido em escoamento em uma tubulação de um ponto A até um ponto B é . Calcule a vazão mássica do fluido nesse escoamento sabendo que (a) o fluido é a água a 20°C (b) o fluido é etanol a 20°C. (c) O escoamento de qual fluido possui maior vazão mássica? Por que?
Dados: ,
Passo 1
Faaala! Para encontrar a vazão mássica a partir da vazão volumétrica, podemos usar essa fórmula aqui:
Mas, essa fórmula só pode ser usada no caso de fluido incompressível (ou seja, um fluido no qual podemos considerar (massa específica) constante.
Ótimas notícias: tanto o etanol quanto a água podem ser considerados incompressíveis aqui nesse exercício, pois a 20°C eles estão na fase líquida. ;D Então vamos fazer essa hipótese de fluido incompressível e utilizar essa fórmula!
No caso da água, . Substituindo:
Logo:
Passo 2
Show! Para calcular a vazão mássica do etanol, vamos usar o mesmo raciocínio, pois o etanol também pode ser considerado incompressível a 20°C.
Sabendo que a massa específica do etanol é e lembrando que a vazão volumétrica é a mesma
Fazendo as contas:
Com isso, encontramos a vazão mássica do escoamento de etanol. :D
Passo 3
Encontramos na letra (a) que a vazão mássica de água é . Na letra b, encontramos que a vazão mássica de etanol é
Então, a maior vazão mássica é do escoamento de água!
E por que isso acontece? Porque nos dois escoamentos temos a mesma vazão volumétrica, mas a água possui massa específica maior que a do etanol (ambos a 20°C). Com isso, pela fórmula , o escoamento de água terá maior maior vazão mássica.
Resposta
(a)
(b)
(c) A água, pois sua massa específica é maior que a do etanol. Além disso, a vazão volumétrica é a mesma.
Exercício Resolvido #2
Uma mangueira de incêndio tem um diâmetro interno de e água está escoando a . O escoamento sai através de um bocal com um diâmetro . Para escoamento permanente, qual deve ser o , em , para haver uma velocidade média de saída de ?
Passo 1
Como o fluido é água então nosso escoamento além de permanente e incompressível.
Assim, a quantidade de água que entra tem que ser igual a que sai.
Então nesse caso nosso volume de controle será a parte da mangueira com diâmetro igual ao indicado no enunciado e o bocal de saída.
Assim iremos escrever a equação do que entra igual ao que sai, da seguinte forma:
A vazão da mangueira foi dada, porém em uma unidade esquisita. Vamos passar essa unidade para que é a padrão.
Para isso basta dividir por , já que um minuto tem .
Assim, temos que:
Como queremos uma velocidade de , a área vai ser:
Agora para descobrir o diâmetro, basta lembrarmos a área de um circulo.
Em milímetros isso vale:
Resposta
Exercício Resolvido #3
Três tubos fornecem água em regime permanente a para um tubo maior de saída mostrado na figura abaixo. A velocidade e a vazão de saída . Encontre , e se sabemos que aumentando em aumentará em .
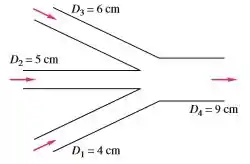
Passo 1
Novamente temos um escoamento em um sistema. E como sabemos que a água é um fluido incompressível a , então temos que a vazão de entrada é igual a vazão de saída. Podemos escrever isso como:
Vamos agora isolar o que temos para um lado e o que não temos para o outro. Como o enunciado deu e (com o qual a gente pode descobrir ), temos:
O problema é que a vazão dada de está em e a velocidade do fluido em foi dada em ,assim precisamos passar a vazão para .
E já que estamos aqui, vamos calcular o e matar logo o item c:
Se liga que a gente passou aquele diâmetro que estava em cm pra metro antes de resolver, falou?
Passo 2
Agora vamos usar o fato que “se sabemos que aumentando em aumentará em ”. Olha só o que isso significa... Atualmente temos que:
Se aumentarmos :
E podemos fazer a segunda equação menos a primeira, obtendo:
Então um aumento de da vazão de água em é igual a um aumento de 0,1 da vazão em .
Como sabemos , conseguimos achar .
Agora para achar a velocidade de vazão basta dividir a vazão pela área.
Passo 3
Finalmente podemos resolver o primeiro item:
Como sabemos , e conseguimos saber o valor de , pois lá no inicio montamos a equação de entradas e saídas do sistema.
Agora, isolando a incógnita , temos:
Substituindo e :
Agora, sabendo a vazão em , facilmente conseguimos descobrir a velocidade média do fluido nessa região:
Resposta
Exercício Resolvido #4
Considere o escoamento incompressível e permanente através do dispositivo mostrado abaixo. Determine o módulo da vazão volumétrica através da abertura e verifique se o fluxo é para fora ou para dentro do dispositivo.
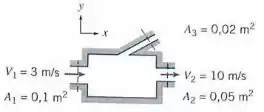
Passo 1
Vimos na teoria que em escoamento incompressível e permanente o que entra tem que ser igual ao que sai, pois o volume do nosso sistema é fixo e nosso fluido é incompressível.
Assim tudo que entra é igual a tudo que sai:
A gente sabe que o fluido entra em e sai em . Porém não temos ideia do que está acontecendo em . Então vamos assumir que esta entrando.
Por que eu fiz isso? A gente precisa montar uma equação com entradas e saídas, certo? Então eu preciso supor que ele é entrada ou saída. Se eu acertar minha suposição o valor que eu achar vai ser positivo. Se eu errar ele vai ser negativo. Então vamos lá.
Vamos montar a equação de entradas e saídas:
Substituindo os valores que temos nas figura, chegamos em:
Opaa, deu positivo, então eu acertei o fluido está entrando.
Resposta
Fluido entrando no sistema.
Exercício Resolvido #5
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011
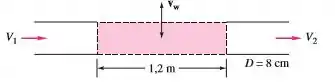
Água escoando por um tubo com de diâmetro entra em uma seção porosa, como mostra a figura abaixo, que permite uma velocidade radial uniforme através das superfícies das paredes por uma distância de . Se a velocidade média na entrada for igual a , determine a velocidade de saída se para fora do tubo ou para dentro do tubo. Qual valor de fará ?
Passo 1
Então galera, esse é um exercício que devemos calcular o balanço de água que entra igual a água que sai, ou seja:
Passo 2
Calcularemos cada vazão separadamente, a começar por que é a mais simples.
Lembramos que a vazão é dada pelo produto da área da seção e da velocidade média do fluido.
Nos é passado que basta então calcular .
Como a área é de um círculo de diâmetro
Logo se :
A vazão possui a mesma área, ou seja,
Então
Agora para a vazão , devemos utilizar outra área para o escoamento.
Como o tubo é cilíndrico devemos calcular a área da superfície de saída/entrada como sendo a casca do cilíndro:
Onde .
O que nos dá uma vazão de:
Passo 3
Na letra a seção porosa trabalha como saída, então:
Sabemos que:
Para :
Logo
Passo 4
Na letra a seção porosa trabalha como entrada, então:
Se :
Passo 5
Para a letra calcularemos dado que :
Como não sabemos se é de entrada ou saída, vou supor que seja de saída:
Repare que nossa suposição estava correta. Caso fosse negativo, seria de entrada.
Resposta
Exercício Resolvido #6
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Quando um jato líquido, regido pela gravidade, sai de uma fenda em um tanque, como na figura abaixo, uma aproximação para a distribuição de velocidade na saída é
onde é a profundidade da linha de centro do jato. Próximo à fenda, o jato é horizontal, bidimensional, e de espessura , como mostrado. Encontre uma expressão geral para a vazão volumétrica total que sai da fenda.
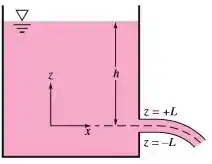
Passo 1
Nesta questão devemos aplicar a expressão que define a vazão que passa por uma área:
No caso a velocidade é e como o jato é bidimensional vamos dizer que
Sendo que é uma largura que “sai” da tela.
Passo 2
Em seguida devemos resolver nossa integral substituindo as informações que temos:
Se ,
Podemos tirar e de dentro da integral:
Vamos realizar a substituição e . (Obs.: nossos limites de integração também vão mudar...Como varia de até , irá variar de até )
Resposta
Exercício Resolvido #7
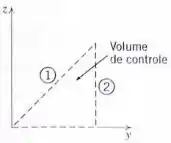
Um campo de velocidade é dado por , onde e . Para o volume de controle triangular de (com profundidade de perpendicular ao diagrama), um elemento de área pode ser representado por e um elemento de área por
Encontre uma expressão para .
Avalie
Encontre uma expressão para
Avalie
Passo 1
Calma galera, essa questão é bem mais simples do que parece.
Vou reescrever o que o enunciado falou, colocando na forma de trios ordenados:
Substituindo os valores de e e tirando a coordenada dos vetores (todas são nulas)
Passo 2
Na letra é pedido para calcularmos :
Fazendo o produto escalar:
Na letra é pedido para calcularmos aquela integral:
Sabemos que e que , logo:
Passo 3
Calculamos outro produto escalar, agora o da letra :
Logo a expressão pedida em :
Resposta
Exercício Resolvido #8
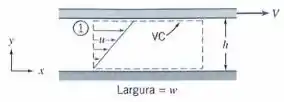
(a) Obtenha expressões para a vazão volumétrica para o fluxo de quantidade de movimento através da secção transversal do volume de controle mostrado no diagrama.
Para o escoamento do item anterior, obtenha uma expressão para o fluxo de energia cinética, , através da seção transversal do volume de controle mostrado.
Passo 1
Para calcularmos a vazão volumétrica devemos utiliza a expressão:
Pela figura temos que o elemento de área é:
E é definido apenas por sua componente horizontal .
Passo 2
Podemos dizer pela figura que
Com as seguintes condições de contorno:
Subsituindo na expressão de :
Logo,
Passo 3
Substituindo na expressão da vazão:
Passo 4
Na letra é pedido para que calculemos o fluxo de energía cinética dado pela fómula:
Subsituindo nossas expressões de e :
Arrumando a casa: