Teorema de Transporte de Reynolds e Princípio da Continuidade
Produzido por Raphael EloiTeoria
Teorema de Transporte de Reynolds
Estamos estudando os fluidos em movimento. Será que algo do que estudamos com sólidos ainda vale?
A resposta é sim, claro que vale. As lei de Newton não deixariam de valer apenas porque o gelo passou a ser água.
Tudo que estudamos vale para as partículas do fluido. Só que em um escoamento na grande maioria das vezes estaremos atrás de um resultado do sistema (englobado no volume de controle) por exemplo: a força de arrasto que a água exerce sobre o casco de um navio. E não na aceleração de uma única partícula de água.
As leis fundamentais que estudamos: Leis de Newton, leis da termodinâmica, quantidade de movimento, conservação de energia, valem então para o Volume de Controle?
Elas valem para o material, valem para uma partícula do fluido, mas não valem para o volume de controle. Mas como assim???

Calma, Watson, que vamos resolver esse mistério. Para usar as leis fundamentais no volume de controle será necessário uma adaptação, uma nova abordagem. E é ai que entra o Teorema de Transporte de Reynolds.
O que esse teorema faz é possibilitar aplicarmos as equações básicas que vimos na teoria passada para o volume de controle. Por meio dele, vamos encontrar:
- Equação da conservação da massa (princípio da continuidade)
- Equação da conservação do momento linear
- Equação da conservação do momento angular
- Equação da conservação da energia
Todas elas válidas para o Volume de Controle!
Nesse tópico vamos mostrar como funciona o teorema de forma geral e como encontrar a equação da conservação da massa para o volume de controle!
Forma geral do teorema
Veremos o teorema para o caso qualquer, em que a forma pode variar e a velocidade do volume de controle pode ser qualquer uma. Para esse caso o teorema de transportes de Reynolds prevê a seguinte equação para adaptar as leis básicas que falamos:
Vamos agora entender o que cada item dessa equação significa.
representa uma propriedade qualquer do fluido. (Para a gente vai variar em massa, quantidade de movimento e energia).
é a sigla para volume de controle. é a derivada da propriedade em relação a massa, assim .
é o infinitésimo de volume.
é a sigla para superfície de controle. Lembra que falei que uma característica do volume de controle seria ter duas superfícies que o fluido iria atravessar fazendo um ângulo , que preferencialmente será . Bem, na fórmula tem um que é , sendo assim é o ângulo que o escoamento faz com o vetor normal (aquele que faz ) a superfície de controle.
é a velocidade relativa entre a velocidade de escoamento do fluido e a velocidade do volume de controle (), onde é a velocidade do fluido e é a velocidade do volume de controle .
Por que preferencialmente seria , por que assim, o escoamento seria normal a superfície de controle e assim e .

Sim, tá quase hahaha Então a equação que temos é a seguinte: A variação da nossa propriedade no tempo é igual a variação dessa propriedade dentro do volume de controle, mais a variação de fluxo dessa propriedade, ou seja, o que sai menos o que entra.
O caso, simples e mais comum que veremos é o caso de um volume de controle fixo, ou seja, tem a forma e posição fixa. Assim o que vai mudar é que como o volume de controle não está se movendo a velocidade dele é zero, assim a velocidade que vemos na equação passa a ser igual a velocidade de escoamento do fluido,
E como a forma é fixa, temos que:
Assim, ficamos com a seguinte equação:
Princípio da continuidade ou Conservação de massa
Até aqui tudo vimos foi a base teórica do que vamos aplicar no futuro. Isso tudo foi desonvolvido com um objetivo: permitir que apliquemos as leis básicas de um sistema para um volume de controle.
É o que começaremos a ver agora, aplicar essa teoria. O primeiro princípio é o de conservação de massa.
Quando tratávamos de um sólido era óbvio que a massa se conservava, mas agora isso não é tão trivial assim.
Então em um sistema em que a massa se conserva, temos que .
Então essa será nossa primeira aplicação do teorema de transporte de Reynolds. Onde a propriedade analisada será a massa. Assim, e .
Então vamos escrever a equação que temos dado um volume de controle qualquer.
Agora, você lembra o que seria se assumirmos uma densidade constante? Lembra que a densidade é massa sobre volume, assim:
Opa, então na verdade temos:
Fazendo a integral de em relação ao volume de controle, temos que:
Agora, como nosso sistema respeita a conservação de massa, temos que , asism chegamos na equação:
O fluxo de entrada é igual ao fluxo de saída.
Lembra que na teoria passada falamos de vazão mássica? Onde a vazão mássica era
E é a vazão volumétrica que foi definida para gente como:
Esse foi o jeito vetorial de se escrever, mas quando estudamos vetores, anos atrás vimos que um produto escalar é igual a:
Assim a vazão mássica é:
Como estamos assumindo um escoamento permanente podemos colocar a densidade para dentro ou fora da integral, assim chegamos que:
Então, nossa equação é a seguinte:
Então dado um volume de controle qualque se somarmos todos fluxos de massa entrando o valor encontrado deve ser igual ao de se somarmos todos os fluxos de massa saindo.
Então vamos fazer um resumo dessa teoria.
Conservação de massa em um escoamento permanente:
Vamos exercitar o que aprendemos? #SoVem
Forma geral do teorema
Princípio da continuidade ou Conservação de massa
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Dado o escoamento de um fluido em um certo volume de controle, encontre a equação do Princípio da Continuidade considerando (a) escoamento permanente (b) escoamento permanente e fluido incompressível.
Passo 1
Esse exercício quer achar a equação da conservação da massa (Princípio da Continuidade) para dois casos que vamos usar muuuito daqui pra frente! Ou seja, vamos usar o resultado desse exercício toda hora. :D
Podemos usar a equação mais geral do princípio da continuidade para começar:
Na letra a do nosso exercício, o escoamento é só permanente. Isso significa que as propriedades não variam com o tempo. Em matematiquês, permanente quer dizer que as derivadas em relação ao tempo são zero, Logo:
Então, a equação do princípio da continuidade fica assim:
Como não temos mais informações para simplificar, essa já é resposta da letra a.
Passo 2
Na letra b, além do escoamento ser permanente (e com isso já podemos usar a última expressão que achamos), o fluido é incompressível.
Fluido incompressível quer dizer que a massa específica é constante! Se é constante, ela não varia e pode sair da integral:
Como se trata do mesmo fluido que está entrando e saindo, podemos cortar
Como não temos mais informações para simplificar, essa é a resposta da letra b 😉
Nos próximos exercícios, vamos aplicar essa equação!
Resposta
a)
b)
Exercício Resolvido #2
Elaboração própria.
Sobre um escoamento permanente de um fluido incompressível em um tanque com uma entrada e duas saídas, analise as seguintes informações e informe se são verdadeiras ou falsas.
I – A massa específica não varia ao longo do escoamento porque se trata de um escoamento permanente.
II – A massa específica varia ao longo do escoamento. Logo,
III – Devido a hipótese de escoamento permanente, as derivadas das propriedades do escoamento em relação ao tempo são zero.
Passo 1
Exercício de verdadeiro ou falso! Vamos lá analisar cada afirmação.
I – A massa específica não varia ao longo do escoamento porque se trata de um escoamento permanente.
A massa específica do fluido de fato não varia ao longo do escoamento. Mas isso acontece porque é um fluido incompressível ( é constante). Logo, a afirmação é falsa, pois a explicação está errada. Próxima!
II – A massa específica varia ao longo do escoamento. Logo,
Acabamos de ver que a massa específica não varia ao longo do escoamento porque é um fluido incompressível. Então, . Muito pelo contrário: . Portanto, afirmação falsa!
III – Devido a hipótese de escoamento permanente, as derivadas das propriedades do escoamento em relação ao tempo são zero.
Lindíssima, falou tudo! Quando consideramos que o escoamento é permanente, queremos dizer que as propriedades não variam com o tempo. Na matemática, isso significa que as derivadas em relação ao tempo são zeradas.
Fique sempre ligado nas hipóteses que o enunciado deixa a gente fazer!
Resposta
I – Falsa
II – Falsa
III – Verdadeira
Exercício Resolvido #3
Fox, R. W., Introdução à mecânica dos fluidos, 7ª ed
Água escoa em regime permanente através de um tubo de comprimento e raio . Calcule a velocidade de entrada uniforme, , se a distribuição de velocidade através da saída é dada por e
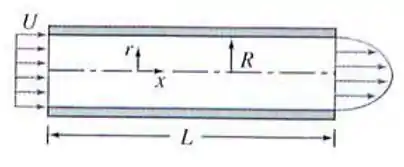
Passo 1
O primeiro passo para resolver qualquer problema de escoamento é listar as características do escoamento que você conhece.
Nesse caso, o nosso escoamento é permanente então:
E incompressível já que o fluido é água. Ser incompressível significa que os fluxos de entrada e de saída de água devem ser iguais.
Assim, pelo que vimos na teoria, se há conservação de massa a equação que usamos é:
Isso para um volume de controle qualquer. Então vamos escolher o nosso de forma a nos ajudar, isso quer dizer com forma e posição fixa. E que as superfícies que atravessam o escoamento façam com o escoamento.
Assim:
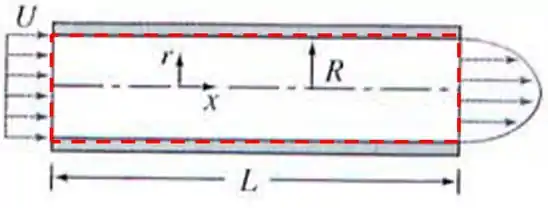
E a equação fica sendo:
Nesse caso , sendo e
Passo 2
Hora de atacar!
Vamos começar colocando as constantes para fora da integral:
Então podemos cortar aquele que apareceu dos dois lados:
Vamos resolver primeiro o lado direito, a integral de é só mesmo:
Passando o para o outro lado e substituindo a área:
Agora, vamos usar uma propriedade das integrais, que a soma de integrais é igual a integral da soma:
Resolver a primeira integral é tranquilo:
Agora, só falta resolvermos a integral difícil, vou até deixar pra outro passo.
Passo 3
Como e não são independentes, não podemos simplesmente tirar o da integral como fizemos antes. A área é a área de um círculo, assim podemos abrir em:
Assim, nossa integral vai virar uma integral de a .
Agora essa integral ficou mais simples, já que temos apenas um polinômio:
Substituindo os limites, temos que a nossa integral é igual a:
Passo 4
Voltando agora a nossa equação temos:
Como é então podemos cortar e , chegando assim:
Assim, chegamos no resultado final, bastando substituir o valor de
Resposta
Exercício Resolvido #4
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 206, ex. P3.15
Água, admitida incompressível, escoa em regime permanente pelo tubo da figura. A velocidade na entrada é constante, , e a velocidade na saída se aproxima do perfil para escoamento turbulento, . Determine a razão para esse escoamento.
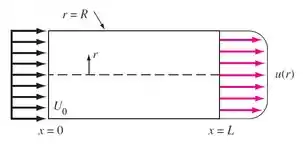
Passo 1
A primeira coisa que o enunciado nos diz é que o escoamento é incompressível e permanente.
Isso simplifica as coisas! Como o escoamento é permanente, .
Então, vimos na teoria que o princípio da continuidade (conservação da massa) para o caso permanente é:
E, como o fluido é incompressível, não varia e posso tirar ele da integral. Vou cortar porque ele está nos dois lados:
O escoamento é todo na horizontal e faz 90° ( com as superfícies de controle. Então, e
são os perfis de velocidade. Vamos ver isso no passo 2!
Passo 2
O enunciado nos informou que a velocidade na entrada é constante e igual a , logo, podemos escrever assim:
A área de entrada é a área A do tubo:
Por outro lado, na saída, o enunciado nos diz que a velocidade não é constante, mas segue esse perfil:
Substituindo:
é a velocidade máxima, um valor constante e que sai da integral:

Vamos ter que resolver essa integral aí? Relaxa, vamos conseguir e estamos aqui para isso! Vamos resolvê-la passo a passo!
Passo 3
Resolvendo a Integral
Primeiro, quem é esse ? Repara que quem está dentro dessa integral depende de r. Além disso, a área de saída é a área de um círculo, então podemos escrever assim:
E a integral fica assim:
Outra coisa importante: aquele 1/7 está elevando todo. Então, não vai dar para separar 1 e r/R tão fácil. Vamos usar a integral por substituição:
A partir daí achamos :
Reorganizando :
Antes de substituir, precisamos atualizar nossos limites
Substituindo, nossa integral vai ficar:
Vamos arrumar isso aí colocando as constantes para fora:
Consertando os limites:
Fazendo a distributiva:
Separando as integrais:

Agora é nosso momento! Vamos integrar!
Fazendo as contas:
E essa integral que a gente está calculando era quem mesmo?
Opa! Encontramos uma expressão para essa integral, que faz parte do princípio da continuidade. Aliás, falando nele, vamos lembrar?
Passo 4
Princípio da continuidade para escoamento incompressível e permanente (vimos no passo 1)
E nos passo 2 e 3, calculamos essas 2 integrais. Substituindo:
Cancelando
Estamos quase lá!!
UHUL! Encontraaaamos a razão para esse escoamento.
Resposta
Exercício Resolvido #5
Uma fina camada de líquido escorrendo sobre um plano inclinado, como na figura abaixo, terá um perfil de velocidades laminar, , em que é a velocidade na superfície. Se o plano tem largura normal ao papel, determine a vazão volumétrica do filme. Suponha que e que a vazão para cada metro de largura do canal seja de . Calcule em .
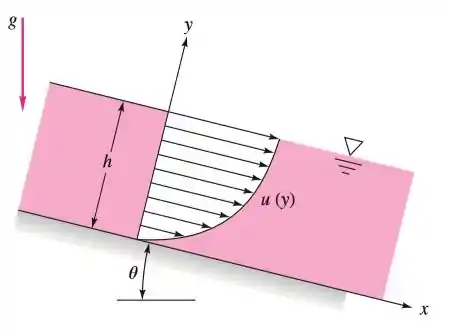
Passo 1
Essa questão é para treinarmos a questão de escolher o volume de controle.
Qual dos dois você acredita ser o melhor? O vermelho ou o azul?
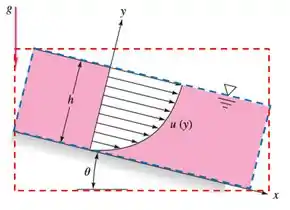
O vermelho está certinho no eixo , sem nenhuma inclinação, porém ele engloba só o liquido e ainda, o liquido escoa pelo volume de controle fazendo um ângulo .
Agora o volume de controle azul, esse está inclinado igual o escoamento, sendo assim engloba apenas o fluido escoando e esse fluido ainda escoa fazendo com a superfície de controle o que já vimos que é muito bom.
Não tem problema inclinarmos o volume de controle, pelo contrario, isso ajuda muito quando o escoamento está inclinado.
Então vamos usar esse volume de controle azul.
Passo 2
Agora vamos calcular o que o enunciado pediu que foi a vazão.
Onde e
Colocando as constantes para fora da integral.
Agora temos duas integrais de polinômio para fazer,
Substituindo agora os limites de integração, temos:
Passo 3
Mas o que queremos é , como temos a vazão podemos substituir na equação da vazão que encontramos. Porém essa unidade de vazão está escrota. Vamos passar para .
Sabemos que e .
Assim, temos:
Agora, podemos substituir na equação que encontramos:
Resposta
Exercício Resolvido #6
O tanque aberto da figura abaixo contém água a e está sendo enchido através da seção . Considere o escoamento incompressível. Primeiro, deduza uma expressão analítica para a taxa de variação do nível d’água, , em termos das vazões e do diâmetro do tanque , arbitrários. Em seguida, se o nível d’água for constante, determine a velocidade na saída, para os dados e .
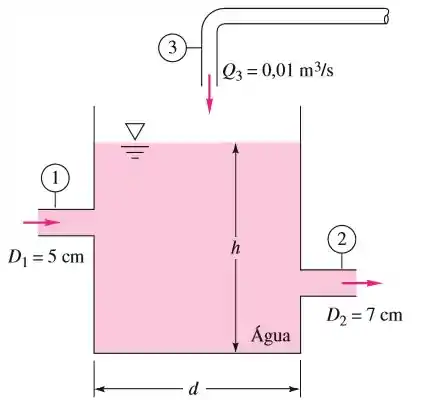
Passo 1
Queremos saber a variação de altura do fluido dado a entrada e saída de fluidos. Para isso vamos analisar a massa do sistema, sabendo que haverá uma conservação de massa, assim se o que entra não é igual ao que sai, essa massa sobrando deve ocupar algum espaço. E será isso que fará varia.
Então vamos montar a equação:
Como a massa do sistema vai se conservar então:
Porém a massa do volume de controle irá variar se o fluxo de entrada for diferente do fluxo de saída. Assim, temos:
Isso era para um volume de controle qualquer, mas agora, vamos escolher nosso volume de controle de forma a nos ajudar.
Ele será fixo, tanto na forma quanto na posição. Assim, vira , e poderemos escrever como vazão o termo: .
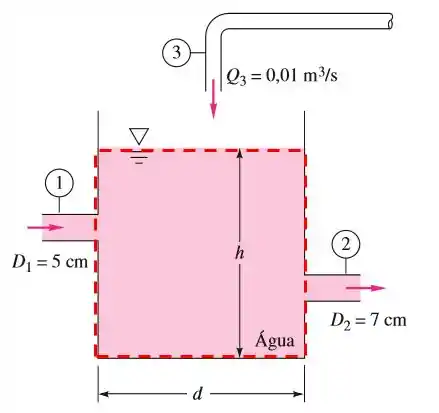
Nosso volume de controle é um paralelepípedo, que terá três superfícies onde haverá fluxo de fluido. As superfícies são as partes que cortam a região .
Vamos reescrever a equação agora colocando em função das vazões:
Podemos colocar a densidade para fora da integral, e a integral do volume de controle será o volume do paralelepípedo, que é
Como só a altura irá variar, então temos:
Cortando a densidade dos dois lados e vendo que o enunciado falou que e são entradas de fluido e é saída, temos:
Chegamos na primeira resposta.
Passo 2
Agora o segundo item quer saber a velocidade se é constante. Assim, .
Para que a igualdade seja mantida, temos que:
Lembrando que
Assim,
Resposta
Exercício Resolvido #7
Considere um tanque de água cilíndrico com área da base igual a e com um orifício de área no fundo, como mostra a figura abaixo. Se a velocidade da água através do orifício é conhecida e igual a e a altura inicial da água no tanque for , determine a altura da água como uma função do tempo .
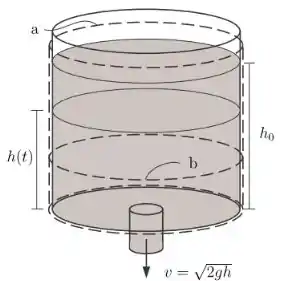
Passo 1
Vamos primeiro escolher o volume de controle. Nosso volume de controle será o tanque cilíndrico. Assim, podemos montar a equação para massa desse escoamento.
Como há conservação de massa então o primeiro termo é zero. E como não há entrada de fluido então o fluxo de entrada também é zero. Assim, só resta:
Como escolhemos um volume de controle fixo e com superfície de saída perpendicular ao escoamento, nosso ângulo será , afinal, esse é o ângulo entre o escoamento e o vetor normal da superfície (nesse caso, ambos apontam para baixo). Usamos então que:
E simplificamos para:
A velocidade foi dada e podemos considerar a densidade constante, então temos:
Vamos resolver as integrais. A primeira é simples é o próprio volume. E a segunda como a integral é em relação a área de saída, então a velocidade pode sair da integral e assim o resultado seria a área de saída. Resultando em:
Colocando o que é constante para fora da derivada temos:
Isolando os temos que tem de um lado, temos:
Integrando dos dois lados temos:
Agora substituindo os limites das integrais temos:
Elevando os dois lados ao quadrado temos: