Exercícios de Teorema de Transporte de Reynolds e Princípio da Continuidade - Lista de Exercícios Resolvida

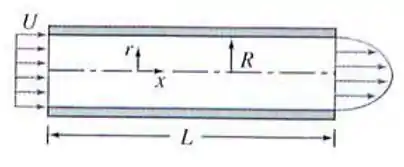
Água, admitida incompressível, escoa em regime permanente pelo tubo da figura. A velocidade na entrada é constante, , e a velocidade na saída se aproxima do perfil para escoamento turbulento, . Determine a razão para esse escoamento.

Sobre um escoamento permanente de um fluido incompressível em um tanque com uma entrada e duas saídas, analise as seguintes informações e informe se são verdadeiras ou falsas.

I – A massa específica não varia ao longo do escoamento porque se trata de um escoamento permanente.

II – A massa específica varia ao longo do escoamento. Logo,

III – Devido a hipótese de escoamento permanente, as derivadas das propriedades do escoamento em relação ao tempo são zero.

Dado o escoamento de um fluido em um certo volume de controle, encontre a equação do Princípio da Continuidade considerando (a) escoamento permanente (b) escoamento permanente e fluido incompressível.

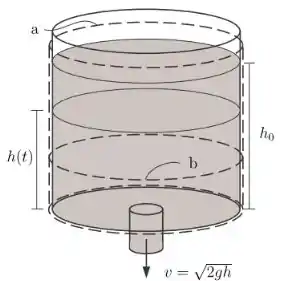
Considere um tanque de água cilíndrico com área da base igual a e com um orifício de área no fundo, como mostra a figura abaixo. Se a velocidade da água através do orifício é conhecida e igual a e a altura inicial da água no tanque for , determine a altura da água como uma função do tempo .

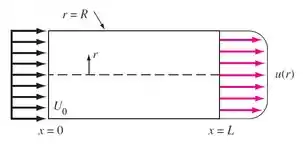
Água escoa em regime permanente através de um tubo de comprimento e raio . Calcule a velocidade de entrada uniforme, , se a distribuição de velocidade através da saída é dada por e

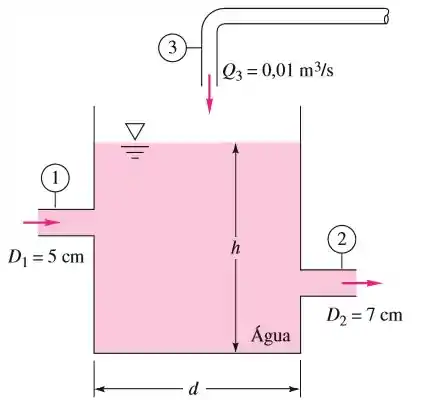
O tanque aberto da figura abaixo contém água a e está sendo enchido através da seção . Considere o escoamento incompressível. Primeiro, deduza uma expressão analítica para a taxa de variação do nível d’água, , em termos das vazões e do diâmetro do tanque , arbitrários. Em seguida, se o nível d’água for constante, determine a velocidade na saída, para os dados e .

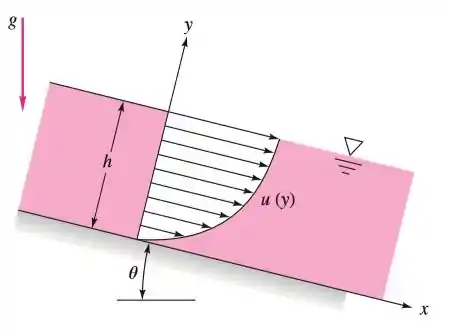
Uma fina camada de líquido escorrendo sobre um plano inclinado, como na figura abaixo, terá um perfil de velocidades laminar, , em que é a velocidade na superfície. Se o plano tem largura normal ao papel, determine a vazão volumétrica do filme. Suponha que e que a vazão para cada metro de largura do canal seja de . Calcule em .