Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 19

Uma chapa fina de vidro de uma janela com 1   m de lado separa o ar quiescente de uma sala a T ∞ , i   =   20 ° C do ar ambiente externo, também quiescente, a T ∞ , e   =   220 ° C . As paredes da sala e a vizinhança externa (paisagens, prédios etc.) estão também a   T v i z , i =   20 ° C e T v i z , e   =   – 20 ° C , respectivamente.

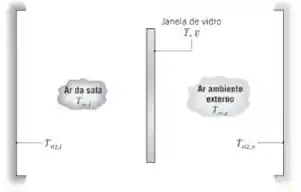
Se o vidro apresenta uma emissividade ε   =   1 , qual é sua temperatura T ? Qual é a taxa de perda de calor através do vidro?

Passo 1

Bora resolver mais uma questãozitcha?! Uhuul. Aqui nós temos as condições de uma sala e do ar ambiente para vidros de janelas. A partir disso, queremos encontrar a temperatura do vidro e a taxa de perda de calor.

Passo 2

Para resolver essa questão vamos assumir:

(1) Condições de estado estacionário;

(2) Gradientes de temperatura são desprezíveis no vidro;

(3) Superfícies internas e externas expostas a grandes ambientes.

Fazendo um balanço de energia no painel da janela, temos:

E ˙ e n t = E ˙ s a i

Ou,

ε σ T s u r , i 4 - T 4 + h i - T ∞ , i - T = ε σ T 4 - T s u r , e 4 + h e - T - T ∞ , e

Onde h i -   e h o - podem ser avaliados por,

N u L - = 0,825 + 0,387   R a L 1 / 6 1 + 0,492 P r 9 / 16 8 / 27 2

Passo 3

Utilizando o Primeiro Modelo de Lei para uma Parede Isotérmica do Plano, a equação do balanço energético foi formulada e resolvida para obter,

T = 273,8 K

A taxa de calor é então,

q i = q e

Ou,

q i = L 2 ε σ T s u r , i 4 - T 4 + h i - T ∞ , i - T

q i = 174,8   W

Resposta

T = 273,8 K

q i = 174,8   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

27 - Repita o Prob.9-26 para uma panela cuja superfície externa é polida e possui uma emissividade de 0,1.
30 - Considere uma placa de circuito impresso (PCI) de 15c m×20c m que possui componentes eletrônicos de um lado.A placa é colocada em uma sala a 20° C .A perda de calor da superfície traseira da plac
Um aquecedor de ambiente de resistência elétrica é concebido de tal modo que lembra uma caixa retangular de 50c m de altura, 80c m de comprimento e 15c m de largura, preenchida com 45k g de óleo. O
Considere uma janela de painel duplo de 1,2m de altura e 2m de largura composta de duas lâminas de vidro ( k =0,78W / m ∙ K ) de 3m m de espessura separadas por um espaço de ar de 2,5c m de largura.
Durante uma visita a uma fábrica, observou-se que a seção vertical da parede da frente de um forno de gás natural de 2m de altura e de 1m de largura era muito quente ao toque. As medidas de temperatur