Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 12
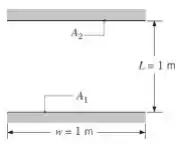
Considere planos paralelos com extensão normal à página infinita como mostrado na figura.
(a) Determine usando os resultados da Figura 13.4.
(b) Determine usando o primeiro caso da Tabela 13.1.
(c) Determine usando o método dos filamentos cruzados de Hottel descrito no Problema 13.6.
(d) Determine usando o segundo caso da Tabela 13.1.
(e) Determine usando os resultados da Figura 13.4, se as dimensões forem aumentadas para
Passo 1
Nessa questão nós temos a geometria de uma placa paralela e queremos encontrar o fator de forma usando os resultados da Figura 13.4, usando o primeiro caso da Tabela 13.1, usando o método de cadeia cruzada de Hottel, usando o segundo caso da Tabela 13.1 e para usando a Figura 13.4.
Passo 2
Para resolver essa questão vamos assumir que o sistema é bidimensional e as superfícies são cinzentas difusas.
Usando a Figura 13.4,
Para o caso 1 da Tabela 13.1,
E,
Passo 3
Do Problema 13.6, temos:
Para o caso 2 da Tabela 13.1,
Por simetria, e pela regra da soma,
Usando a Figura 13.4,