111 - Um tanque esférico de parede dupla de de diâmetro interno é utilizado para armazenar água com gelo a . Cada parede tem de espessura, e o espaço de ar de de espessura e é evacuado de forma a minimizar a transferência de calor. As superfícies vizinhas do espaço evacuado são polidas de modo que cada superfície tenha emissividade de . A temperatura da parede externa do tanque é medida em . Supondo que a parede interna do tanque de aço está a , determine (a) a taxa de transferência de calor para a água gelada no tanque e (b) a quantidade de gelo a que derrete durante o período de 24 horas.
Passo 1
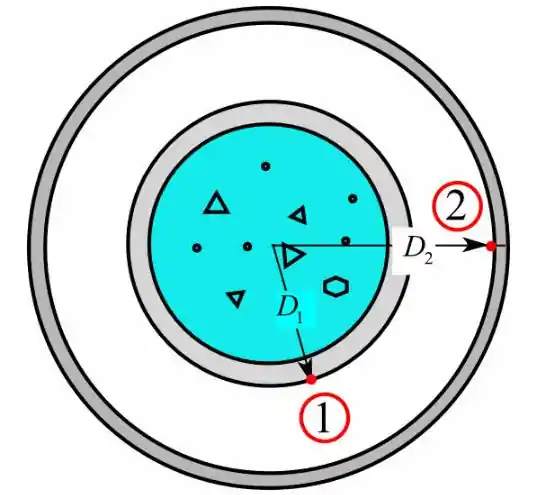
Desenhe o diagrama esquemático do tanque esférico de parede dupla.
Passo 2
Calcule o diâmetro correspondente à superfície (1).
Aqui, o diâmetro da concha interna é e a espessura da concha esférica interna é .
Calcular o diâmetro correspondente à superfície (2).
Aqui é a espessura do vácuo entre as duas conchas.
Passo 3
(a)
Negligencie o calor perdido devido à condução do material da carcaça esférica devido à menor espessura.
Escreva a relação para a taxa de calor transferida para a água gelada.
Aqui, é a área da superfície do tanque esférico, é a constante de Stefan Boltzmann, as temperaturas nas superfícies (1) e (2) são e respectivamente, e a emissividade nas seções (1) e (2) são e respectivamente.
Substituindo pelos valores conhecidos, temos:
Portanto, a taxa de calor transferido para a água gelada é .
Passo 4
b)
Calcule a quantidade de calor transferida para o período de 24 horas.
Passo 5
Calcule a massa de gelo que derrete durante 24 horas.
Aqui, o calor latente da fusão da água é .
Logo,
Assim, a massa de gelo que derrete durante 24 horas é .
Resposta
A taxa de calor transferido para a água gelada é e a massa de gelo que derrete durante 24 horas é de .