Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 12.Problemas - Ex. 69
Um pirômetro de duas cores é um dispositivo que é usado para medir a temperatura de uma superfície difusa, . O dispositivo mede a intensidade direcional espectral emitida pela superfície em dois comprimentos de onda distintos, separados por . Calcule e represente graficamente a razão entre as intensidades e como uma função da temperatura da superfície no intervalo , para e e . Comente sobre a sensibilidade em relação à temperatura e se a razão depende da emissividade da superfície. Discuta os compromissos associados à especificação dos vários valores de . Sugestão: A variação da emissividade em pequenos intervalos de comprimentos de onda é modesta para a maioria dos sólidos, como evidente na Figura 12.17.
Passo 1
Opa, beleza?
Vamos resolver mais uma questão juntos!
Se ajeita aí e bora lá!
Começamos o nosso problema adotando que a superfície é quente em relação ao ambiente, de modo que a reflexão é insignificante em à emissão.
A intensidade espectral emitida pela superfície é:
Assumindo que a emissividade espectral é independente do comprimento de onda sobre , a razão de intensidade, , é:
Passo 2
Dados:
E
e
A variação de ao longo do intervalo é mostrada no gráfico abaixo:
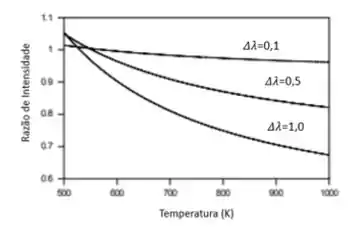
Até a próxima questão!