Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 12.Problemas - Ex. 59

Radiação deixa um forno, que tem temperatura superficial interna de 1500   K , através de uma abertura com 20   m m de diâmetro. Uma porção dessa radiação é interceptada por um detector que se encontra a uma distância de 1   m da abertura, tem uma área superficial de 10 – 5   m 2 e está orientado conforme ilustrado.

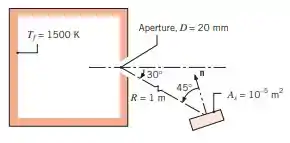
Se a abertura estiver aberta, qual é a taxa na qual a radiação que deixa o forno é interceptada pelo detector? Se a abertura estiver coberta com um material difuso e semitransparente cuja transmissividade espectral seja τ λ = 0,8 para λ ≤ 2   μ m e τ λ = 0 para λ > 2   μ m , qual será a taxa na qual a radiação que deixa o forno é interceptada pelo detector?

Passo 1

E aí, beleza?

Pronto para resolver essa questão comigo?

Vamos lá!

O problema nos pede primeiramente a taxa na qual a radiação que deixa o forno é interceptada pelo detector se a abertura estiver aberta. Utilizaremos a seguinte equação para isso:

q = I c A a cos ⁡ θ 1 ω s - a

q = I c π D 2 4 cos ⁡ θ 1 ω s - a

Calculando I c :

I c = E b T π = σ T f 4 π = 5,67 × 10 - 8 ⋅ 1500 4 π = 9,14 × 10 4   W / m 2 ⋅ s r

Calculando ω s - a :

ω s - a = A n r 2 = A s ⋅ cos ⁡ θ 2 r 2 = 10 - 5 ⋅ cos ⁡ 45 ° 1 2 = 0,707 × 10 - 5   s r

Substituindo os dados na primeira equação que expomos:

q = 9,14 × 10 4 ⋅ π ⋅ 0,02 2 4 ⋅ cos ⁡ 30 ° ⋅ 0,707 × 10 - 5

q = 1,76 × 10 - 4   W

A primeira parte foi resolvida!

Passo 2

Agora, consideraremos se abertura estiver coberta com um material difuso e semitransparente cuja transmissividade espectral seja τ λ = 0,8 para λ ≤ 2   μ m e τ λ = 0 para λ > 2   μ m . Devemos calcular qual será a taxa na qual a radiação que deixa o forno é interceptada pelo detector.

q = τ I e A a cos ⁡ θ 1 ω s - a

q = τ I e π D 2 4 cos ⁡ θ 1 ω s - a

Sendo τ a transmissividade da janela à radiação emitida pela parede do forno, temos:

τ = ∫ 0 ∞ τ λ G λ d λ ∫ 0 ∞ G λ d λ = ∫ 0 ∞ τ λ E λ , b T f d λ ∫ 0 ∞ E λ , b d λ = 0,8 ∫ 0 2 E λ , b E b d λ = 0,8 F 0 → 2   μ m

Com:

λ T = 2 ⋅ 1500 = 3000   μ m ⋅ K

Pela Tabela 12.2:

F 0 → 2   μ m = 0,273

Assim:

τ = 0,8 ⋅ 0,273 = 0,218

Substituindo na equação de taxa de energia:

q = 0,218 ⋅ 1,76 × 10 - 4

q = 0,384 × 10 - 4   W

E assim a gente finaliza a nossa questão!

Até a próxima!

Resposta

q = 1,76 × 10 - 4   W

q = 0,384 × 10 - 4   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma amostra muito pequena de uma superfície opaca encontra-se inicialmente a 1200K e tem a absortividade hemisférica espectral mostrada na figura.A amostra é colocada no interior de um grande comparti
Placas quadradas, após serem borrifadas com uma tinta epóxi, devem ser curadas a 140 ° C por um período de tempo prolongado. As placas estão localizadas em um grande compartimento e são aquecidas por
Um dispositivo para o processamento de materiais com laser utiliza uma amostra em forma de um disco, com diâmetro D=25m m e espessura w=1m m . A amostra tem uma superfície difusa, cuja distribuição es
Um termógrafo de infravermelho (IV) é um radiômetro que fornece uma imagem de um cenário alvo, indicando a temperatura aparente dos elementos no cenário em termos de uma escala de brilho branco e pret
Um processo de fabricação envolve o aquecimento de longos bastões de cobre, que são revestidos com uma fina película, em um grande forno cujas paredes são mantidas a uma temperatura elevada T p . O fo