12-143 Ar de uma sala a e é retirado de forma constante por uma bomba a vácuo através de um tubo adiabático com 3 cm de diâmetro, 2 m de comprimento e
um bocal convergente na entrada. O escoamento na seção do bocal pode ser considerado isentrópico. A pressão estática medida é 97 kPa na entrada do tubo e 55 kPa na saída do tubo.
Determine a vazão de ar através do duto, a velocidade do ar na saída do duto e o fator de atrito médio do duto.
Passo 1
Bora então pegar as informações do enunciado e fazer um esqueminha pra visualizar a questão melhor:
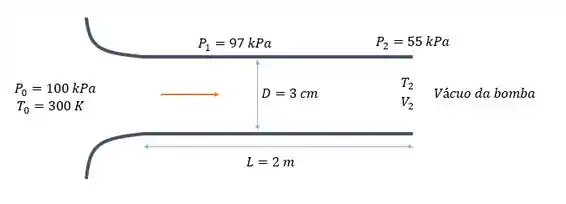
O que temos aqui é um escoamento de Fanno e queremos encontrar a vazão do ar que ta saindo da sala pelo duto, , a velocidade de saída, e o fator de atrito médio, !
Vamos nos concentrar em achar primeiro!! Sabendo que:
Mas não conhecemos nem nem !! Vamos atrás deles para calcular !!!
Passo 2
Se considerarmos o comportamento do ar como gás ideal:
E vamos lembrar também que o escoamento é isentrópico, assim podemos achar :
Como não conhecemos , temos que usar:
Lembrando que para o ar :
Agora podemos achar :
Lembrando que , podemos calcular :
Passo 3
Agora só falta !!! Lembrando que:
Calculamos :
E :
E finalmente vamos achar :
Calculando:
Uhuuuul!! Uma parte já foi!!!
Passo 4
Agora queremos !!!
A gente já conhece e sabemos que estamos lidando com um escoamento de Fanoo de um gás ideal com , então podemos usar a tabela no final do livro para encontrar relações que vão ajudar a gente achar !!!
Na verdade é com essa tabela a gente também pode encontrar , então dois coelhos em uma cajadada só!!!
Para :
Vamos usar a relação das pressões porque conhecemos e é a maneira mais fácil de chegar até :
Substituindo em :
Corremos na tabela e achamos :
E as outras relações também:
Podemos achar :
Conhecemos a gente achou ele lá atrás:
Para encontrar :
Lembrando que e :
Achamos:
Aweee!!