Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas - Ex. 25

O canal em triângulo equilátero na figura abaixo tem declividade S0 constante e um coeficiente n de Manning constante. Determine Q m á x e V m á x . Em seguida, por analogia com a figura 10.6b, trace graficamente as razões Q / Q m á x e V / V m á x em função de y / a para toda a faixa de 0 < y / a < 0,866 .

Passo 1

Fala aí, galera!!! Bora pra mais um “lerigou” da mecânica dos fluidos? Bem, vamos lá, como se trata de um triângulo equilátero, resolver esse k.o aí não deve ser tão complicado. Vamos então tentar calcular nossa velocidade V e nossa vazão Q!!

Passo 2

A gente sabe que

Q = 1 n A R h 2 3 S o 1 2

E que V A = Q → Q A = V

V = 1 n R h 2 3 S o 1 2

Onde temos que R h = A P

Passo 3

Bora calcular a área desse canal que está com fluido dentro, beleza?

Note que no nosso desenho, a área que está preenchida tem o formato de um trapézio, então podemos pensar que a área também pode ser calculada pela área de um trapézio!!!

A = a 2 2 s e n θ - 1 - y a s e n θ 2 = a 2 2 0,866 - 1 - y 2 0,866 a 2

Passo 4

O perímetro pode ser calculado como sendo:

P = a + 2 a 1 - y 0,866 a

E finalmente Q = V A

A velocidade máxima e a vazão podem ser calculadas como sendo:

V m á x = 0,301 a 2 3 n S o 1 2 em y a = 0,54

Q m á x = 0,123 a 8 3 n S o 1 2   em y a = 0,74

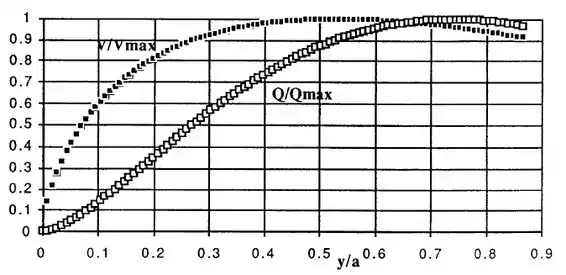
O gráfico fica assim ó:

 

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Reconsidere o Problema 13-50. Se a altura máxima de escoamento que o canal consegue acomodar é 2,4m , determine a vazão máxima de escoamento através do canal.
Considere o escoamento de água através de dois canais 13-52 idênticos com seções de escoamento quadradas de 3mx3m . Agora os dois canais são combinados, formando um canal com 6m de largura. A vazão é
Um canal trapezoidal com uma largura do fundo de 5m , largura de superfície livre de 10m , e profundidade de escoamento de 2,2m descarrega água a uma vazão de 120m 3 / s . Se as superficies do canal e
Água deve ser transportada em um canal aberto, cujas superfícies são revestidas com asfalto, uma taxa de 4m 3 / s no escoamento uniforme. A inclinacão inferior é 0,0015 . Determine as dimensões da mel
Um sistema de drenagem de água com inclinação constante de 0,0015 deve ser construido com três canais circulares feitos de concreto polido dois dos canais em diâmetro de 1,2m e drenam para um terceiro