Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 126

126. Uma corrente de ar atmosférico é usada para secar uma série de amostras biológicas sobre placas que possuem, cada uma, um comprimento de Li = 0,25 m na direção do escoamento do ar. O ar está seco e a uma temperatura igual a das placas (T∞ = Ts = 50°C). A velocidade do ar é u∞ = 9,1 m/s.

(a) Esboce a variação do coeficiente de transferência de massa local hm,x com a distância x da aresta frontal. Indique a natureza específica da dependência em x.

(b) Qual das placas irá secar mais rápido? Calcule a taxa de secagem por metro de largura nesta placa (kg/(s · m)).

(c) A que taxa calor deveria ser fornecido à placa que seca mais rápido para mantê-la a Ts = 50°C durante o processo de secagem?

Passo 1

Letra (a)

Primeiro devemos calcular qual é o Reynolds neste caso, sendo assim:

R e x = u ∞ x v       ( 1 )

Em que temos para o valor de transição do número de Reynolds um valor de

R e x = 5 × 10 5

Obtenha as propriedades de, "Propriedades termo-físicas da matéria da tabela A-4 no ar  323   K ".

v = 18,2 × 10 - 6 m 2 s

Obtenha as propriedades de, "Propriedades termo-físicas da água da Tabela A-4 da matéria em  323 K ".

ρ A , s a t = 0,0256   k g / m 3

h f g = 2438   k J / k g

ρ ∞ = 0   k g / m 3  

D A B = 2,93 × 10 - 5     m 2 / s  

Obtenha as propriedades de, "Propriedades termo-físicas da água da Tabela A-4 da matéria em  288   K ".

D A B 2 = 0,26 × 10 - 4 m 2 s

Agora devemos calcular o número de Schmidt

S c = v D A B

= 18,2 × 10 - 6 2,93 × 10 - 5

= 0,621

Substituindo os valores na equação (1) vem:

5 × 10 5 = ( 9,1 ) x 18,2 × 10 - 6

x = 1 m

Calcule o número de Sherwood usando a equação 7.26 do livro.

S h x = 0,332 R e x 1 2 S c 1 3

= 0,332 5 × 10 5 1 2 0,621 1 3

= 200,18

Escreva a relação geral para o número Sherwood para a partir daí obtermos o coeficiente h.

S h x = h m x D A B

200,18 = h m 1 m 2,93 × 10 - 5   m 2 s

h m = 5,865 × 10 - 3   m / s

Calcule os valores de transferência de massa para os valores restantes de   x   da mesma maneira.

Desenhe a tabela com vários valores de coeficiente de transferência de massa e  x .

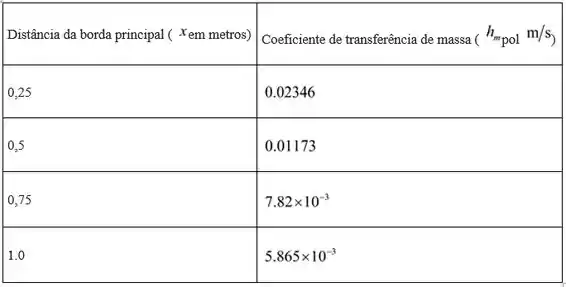
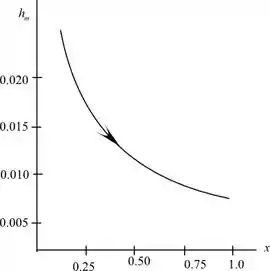
Desenhe os gráficos entre as distâncias da borda anterior ao coeficiente de transferência de massa local.

Passo 2

Letra (b)

A partir do diagrama, a primeira ou a quinta placa secará mais rapidamente devido à associação da maior evaporação com as placas seguintes.

Calcule o número de Reynolds para o primeiro prato.

R e x 1 = u ∞ x 1 v

= 9,1 × 0,25 18,2 × 10 - 6

= 12,5 × 10 4

Escreva a relação para calcular a taxa de evaporação.

n A 1 = h - m 1 A s 1 ρ s - ρ ∞     ( 2 )

Só que nesse caso não temos o coeficiente h, então escreva a relação para calcular o coeficiente de transferência de massa usando a relação para a placa 1.

h - m 1 = D A B 1 x 1 0,664   R e x 1 2 × S c 1 3

= 0,26 × 10 - 4 m 2 s 0,25   m 0,664 × 12,5 × 10 4 1 2 × 0,621 1 3

= 0,02083 m s

Substituindo tudo na equação (2):

n A 1 = h - m 1 A s 1 ρ s - ρ ∞

= 0,02083 m s 1 m × 0,25 m 0,082 k g m 3 - 0

= 4,27 × 10 - 4 k g s

Escreva a relação para calcular a taxa de evaporação na quinta placa

n A 5 = h - m 0 - 5 A s 0 - 5 ρ s - ρ ∞ - h - m 0 - 4 A s 0 - 4 ρ s - ρ ∞     ( 3 )

Só que nesse caso não temos o coeficiente h, então escreva a relação para calcular o coeficiente de transferência de massa usando a relação para a placa 1.

h - m 0 - 5 = D A B 1 x 5 0,037   R e x 5 4 5 - 871 S c 1 3       ( 4 )

Calcule o número de Reynolds para o primeiro prato.

R e x 5 = u ∞ x 5 v

= 9,1 × 1,25 18,2 × 10 - 6

= 62,5 × 10 4

Substituindo na equação (4):

h - m 0 - 5 = D A B 1 x 5 0,037   R e x 5 4 5 - 871 S c 1 3

= 0,26 × 10 - 4 m 2 s 1,25   m 0,037 × 62,5 × 10 4 4 5 - 871 0,621 1 3

= 0,0141 m s

Escreva a relação para calcular o coeficiente de transferência de massa usando a relação para a placa 0-4.

h - m 0 - 4 = D A B 1 x 4 0,664   R e x 4 4 2 × S c 1 3   ( 5 )

Calcule o número de Reynolds para a quarta placa.

R e x 5 = u ∞ x 5 v

= 9,1 × 1 18,2 × 10 - 6

= 50 × 10 4

Substituindo na equação (5):

h - m 0 - 4 = 0,26 × 10 - 4 m 2 s 1   m 0,664 × 50 × 10 4 4 5 × 0,621 1 3

= 0,0108 m s

Substituindo todos os valores encontrados na equação (3):

n A 5 = 0,0141 m s ( 1,25 m 2 ) 0,082 k g m 3 - 0 - 0,0108 m s ( 1 m 2 ) 0,082 k g m 3 - 0

= 5,24 × 10 - 4 k g s

Como o coeficiente de transferência de massa na quinta placa é maior, a taxa de evaporação é maior na quinta placa.

Calcule a taxa de secagem por metro de largura.

n A 5 = 5,24 × 10 - 4 k g s W

= 5,24 × 10 - 4 k g m .   s

Portanto, a taxa de evaporação por unidade de largura é   5,24 × 10 - 4 k g m .   s  .

Passo 3

Letra (c)

Escreva a relação para Calcular a taxa de transferência de calor na placa de secagem mais rápida.

q 5 = n A 5 h f g

= 5,24 × 10 - 4 k g m .   s 2383 k J k g

= 1250,59 W m

Portanto, a taxa de transferência de calor para a placa de secagem mais rápida é  1250,59 W m .

Resposta

  1. Gráfico
  2. 5, 5,24 × 10 - 4 k g m .   s
  3. q 5 = 1250,59 W m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

140 - O problema de poluição térmica está associado à descarga de água quente de plantas de potência elétrica ou de fontes industriais em um corpo natural de água. Métodos para minimizar esse problema
142 - Uma gota de água esférica com 0,5m m de diâmetro cai a uma velocidade de 2,15m / s através de ar seco em repouso a uma pressão de 1a t m . Estime a taxa instantânea de evaporação na gota, com a
143 - Uma gotícula esférica de álcool, com 0,5m m de diâmetro, cai livremente através de ar em repouso a uma velocidade de 1,8m / s . A concentração de vapor de álcool na superfície da gotícula é de 0
146 - Em um sistema de umidificação de um forno doméstico, gotículas de água com diâmetro D são descarregadas na direção e em sentido oposto ao movimento do ar quente que emerge do aquecedor. O ar é u
141 - Oxicocos (cranberries) são colhidos pelo alagamento dos atoleiros nos quais eles crescem e são classificados em tonéis para o transporte. Na planta de processamento, a umidade superficial dos fr