Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 14
14. Experimentos para determinar o coeficiente de transferência de calor por convecção local em um escoamento uniforme e normal a um disco circular aquecido forneceram uma distribuição radial para os números de Nusselt na forma
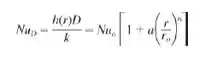
sendo n e a positivos. O número de Nusselt no ponto de estagnação é correlacionado em termos dos números de Reynolds (ReD = VD/v) e de Prandtl
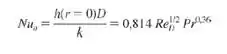
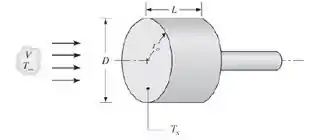
Obtenha uma expressão para o número de Nusselt médio, = D / k, correspondente à transferência de calor em um disco isotérmico. Tipicamente, o desenvolvimento de uma camada-limite a partir de um ponto de estagnação fornece um coeficiente convectivo decrescente com o aumento da distância a partir do ponto de estagnação. Forneça uma explicação plausível para o fato de se ter observado uma tendência oposta para o disco.
Passo 1
Calcule o coeficiente médio de transferência de calor dado por:
Substituindo na expressão chegamos em:
Como,
Substitua por .
Assim, o número médio de Nusselt é
Passo 2
O aumento de h (r) com r pode ser descrito em termos de curva acentuada, que o fluxo da camada limite deve suportar em torno da borda do disco. A camada limite acelera e sua espessura diminui à medida que faz a curva. Isso faz com que o coeficiente de convecção local aumente.