Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 101

13-101 Repita o Problema 13-100 para uma profundidade de escoamento a montante de 2,2 m.

Passo 1

Vamos nessa!! O enunciado pede pra a gente repetir o que a gente fez no problema anterior, mas mudando a profundidade y 1 que dessa vez é y 1 = 2,2   m .

No problema anterior tinhamos um escoamento com um reservatório triangular, assim:

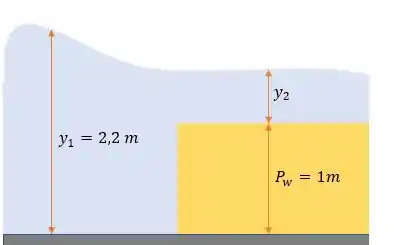
A largura do reservatório é b = 5 m e queriamos achar a vazão do reservatório e a profundidade mínima y 2 e isso que vamos fazer de novo!

Para calcular a vazão usamos essa fórmula aqui:

V ˙ r e c = C w d , r e c   2 3 b 2 g   H 3 2

calculando a carga do reservatório, H :

H = y 1 - P w = 2,2 - 1 = 1,2

Agora falta conhecermos o coeficiente de descarga, C w , r e c !

Passo 2

Vamos calcular C w , r e c da seguinte forma:

C w , r e c = 0,65 1 + H P w

Substituindo os valores:

C w , r e c = 0,65 1 + 1,2 1 = 0,514

Agora sim! Podemos calcular a vazão:

V ˙ r e c = 0 , 514 × 5 × 9,81 × 2 3 3 2 × 1,2 3 2

Calculando:

V ˙ r e c = 4,91   m 3 / s

Passo 3

Agora queremos achar o a profundidade mínima, y 2 , como falamos no problema anterior, isso acontece no ponto crítico, quando y 2 = y c , então:

y 2 = y c = V ˙ 2 g b 2 1 3

Podemos substituir e calcular:

y 2 = 4 , 91 2 9,81 × 5 2 1 3 = 0 , 462   m

Prontinhooo!

Resposta

V ˙ r e c = 4 , 91   m 3 / s

y 2 = 0 , 462   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13-105 Água escoa era ura canal a uma velocidade média de 4 m/s. Determine se o escoamento é subcrítico ou supercrítico para profundidades de escoamento de (a) 0,2 m, (b) 2 m e (c) 1,63 m.
Um reservatório de soleira espessa com 1 m de altura é usado para medir a vazão da água em um canal retangular com 5 m de largura. A profundidade de escoamento bem a montante do reservatório é de 1,6
Considere o escoamento da água em um reservatório de soleira espessa com 0,80 m de altura e suficientemente longo. Se a profundidade mínima de escoamento acima do reservatório for medida como 0,50 m,
Considere o escoamento de água através de um canal retangular largo que sofre um salto hidráulico. Mostre que a razão entre os números de Froude antes e depois do salto pode serexpressa em termos das
13-113 Considere dois canais idênticos, uma retangular com largura de fundo b e outro circular com diâmetro D e vazões de escoamento, inclinações de fundo e revestimentos de superfícieidênticos. Se a