13.55 Duas esferas concêntricas com diâmetro D1 = 0,8 m e D2 = 1,2 m estão separadas por um espaço contendo ar e têm temperaturas superficiais de T1 = 400 K e T2 = 300 K.
- Se as superfícies forem negras, qual é a taxa de troca de radiação líquida entre as esferas?
- Qual é a taxa de troca de radiação líquida entre as superfícies se elas forem difusas e cinzas com ε1 = 0,5 e ε2 = 0,05?
- Qual é a taxa de troca de radiação líquida se o valor de D2 for aumentado para 20 m, com ε2 = 0,05; ε1 = 0,5 e D1 = 0,8 m? Qual seria o erro introduzido caso fosse admitido um comportamento de corpo negro para a superfície externa (ε2 = 1), com todas as demais condições permanecendo as mesmas?
- Para D2 = 1,2 m e emissividades de ε1 = 0,1; 0,5 e 1,0; calcule e represente graficamente a taxa de troca de radiação líquida como uma função de ε2 para 0,05 ≤ ε2 ≤ 1,0.
Passo 1
Vamos lá! Pra começar, vamos desenhar um esqueminha do que o enunciado ta dizendo:
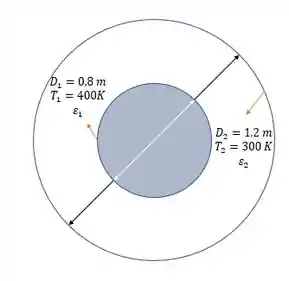
Para a letra as superfícies são negras, logo , queremos a taxa de troca de radiação líquida entre as duas esferas:
Onde :
Pela regra da soma:
Se , então:
Sabendo que :
Achamos:
Passo 2
Agora a gente quer mas as emissividades são e , temos esferas concêntricas, logo podemos usar a equação do livro:
Podemos substituir:
Achamos:
Passo 3
Agora temos a seguinte situação:
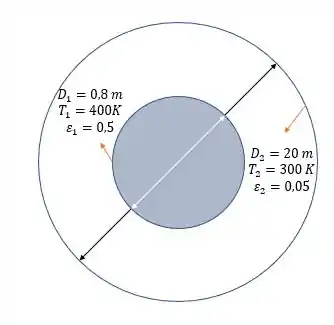
E queremos !! Vamos usar a mesma equação que usamos no Passo 2 e só temos que mudar um dado, .
Calculando:
Mas também queremos saber o erro, caso a gente considerasse , então vamos calcular para esse caso:
O erro é dado por:
Substituindo:
Achamos:
Passo 4
E por fim, a gente volta para as dimensões originais, onde e a gente quer ver graficamente a relação entre e para três valores diferentes de :
Mas primeiro vamos calcular
Simplificando:
Com isso vamos plotar o gráfico variando entre e
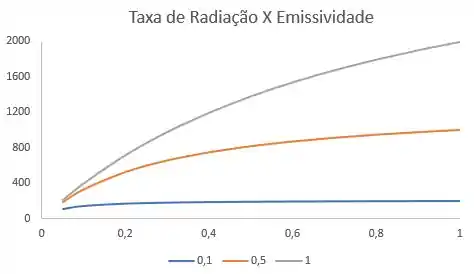
Aweeeee!
Resposta
Ei, a resposta está no passo a passo :)