Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 64

Uma barreira de radiação difusa e cinza, com 60 mm de diâmetro e emissividades ε2,i = 0,01 e ε2,e = 0,1 nas superfícies interna e externa, respectivamente, é concêntrica a um longo tubo que transporta um fluido de processo quente. A superfície do tubo é negra e tem um diâmetro de 20 mm. Há vácuo na região interna da barreira. A superfície externa da barreira está exposta a uma grande sala, cujas paredes estão a 17°C, e experimenta transferência de calor por convecção com o ar a 27°C, com um coeficiente de transferência de calor por convecção de 10 W/(m2·K).

Determine a temperatura de operação do tubo interno se a temperatura da barreira for mantida a 42°C.

Passo 1

Vamos fazer um esqueminha do que o enunciado ta dizendo:

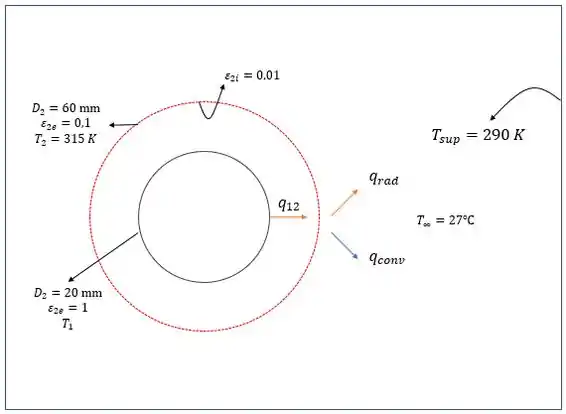
A gente quer decobrir quem é T 1 , então vamos ver como a gente chega nele!!

Fazendo um balanço das taxas de calor, temos:

q 12 = q c o n + q r a d

Em q 12 temos dois tubos concêntrico, nesse caso escrevemos:

q 12 = σ A 1 T 1 4 - T 2 4 1 ε 1 + 1 - ε 2 i ε 2 i D 1 D 2

Opaa, o T 1 apareceu!!!

q c o n v   pode ser escrito como:

q c o n v = h A 2 ( T 2 - T ∞ )

E q r a d :

q r a d = ε 2 e A 2 σ ( T 2 4 - T s u p 4 )

Igualanaod:

σ A 1 T 1 4 - T 2 4 1 ε 1 + 1 - ε 2 i ε 2 i D 1 D 2 = h A 2 T 2 - T ∞ + ε 2 e A 2 σ ( T 2 4 - T s u p 4 )

Isolando T 1 :

T 1 = T 2 4 + h A 2 T 2 - T ∞ + ε 2 e A 2 σ T 2 4 - T s u p 4 σ A 1 × 1 ε 1 + 1 - ε 2 i ε 2 i D 1 D 2 1 4

Isolando as áreas:

T 1 = T 2 4 + A 2 A 1 h T 2 - T ∞ + ε 2 e σ T 2 4 - T s u p 4 σ × 1 ε 1 + 1 - ε 2 i ε 2 i D 1 D 2 1 4

Passo 2

Relembrando os dados do enunciado:

h = 10   W / m 2 K

T s u p = 17 ℃ + 273 = 290   K

T ∞ = 27 ° + 273 = 300   K

T 2 = 42 ℃ + 273 = 315 ℃

ε 2 i = 0,01

ε 2 e = 0,1

ε 1 = 1

A 2 A 1 = D 2 D 1 = 60 20

Sabendo que σ = 5,67 × 10 - 8 W / m 2 K 4 , vamos substituir:

T 1 = 315 4 + 60 20 h 315 - 300 + 0,1 × 5,67 × 10 - 8 315 4 - 290 4 σ × 1 1 + 1 - 0,01 0,01 20 60 1 4

T 1 = 749   K

Ou:

T 1 = 472 ℃

Uhuuuul!!!

Resposta

T 1 = 472 ℃

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13.54 Oxigênio líquido é armazenado em um vaso esférico com parede delgada e 0,8 m de diâmetro, que encontra-se no interior de um segundo vaso esférico, também com parede delgada e com 1,2 m de diâmet
No fundo de uma grande câmara de vácuo cujas paredes estão a 300 K, um painel negro com 0,1 m de diâmetro é mantido a 77 K. Para reduzir o calor ganho nesse painel, uma barreira de radiação com o mesm
Um forno está localizado próximo a um denso conjunto de tubos de transporte de um fluido criogênico. O conjunto de tubos cobertos por gelo formam aproximadamente uma superfície plana com uma temperatu
13.53 Um condutor elétrico muito longo, com 10 mm de diâmetro, está posicionado concentricamente no interior de um tubo cilíndrico resfriado, com 50 mm de diâmetro, cuja superfície é difusa e cinza co
Transferência de calor por radiação ocorre entre duas grandes placas paralelas, que são mantidas a temperaturas T1 e T2, com T1T2. Para reduzir a taxa de transferência de calor entre as placas, propõe